Предмет: Алгебра,
автор: D3dMak51m
Найти решение задачи Коши, используя метод операционного
исчисления.
Приложения:

Ответы
Автор ответа:
1
Объяснение:
Приложения:
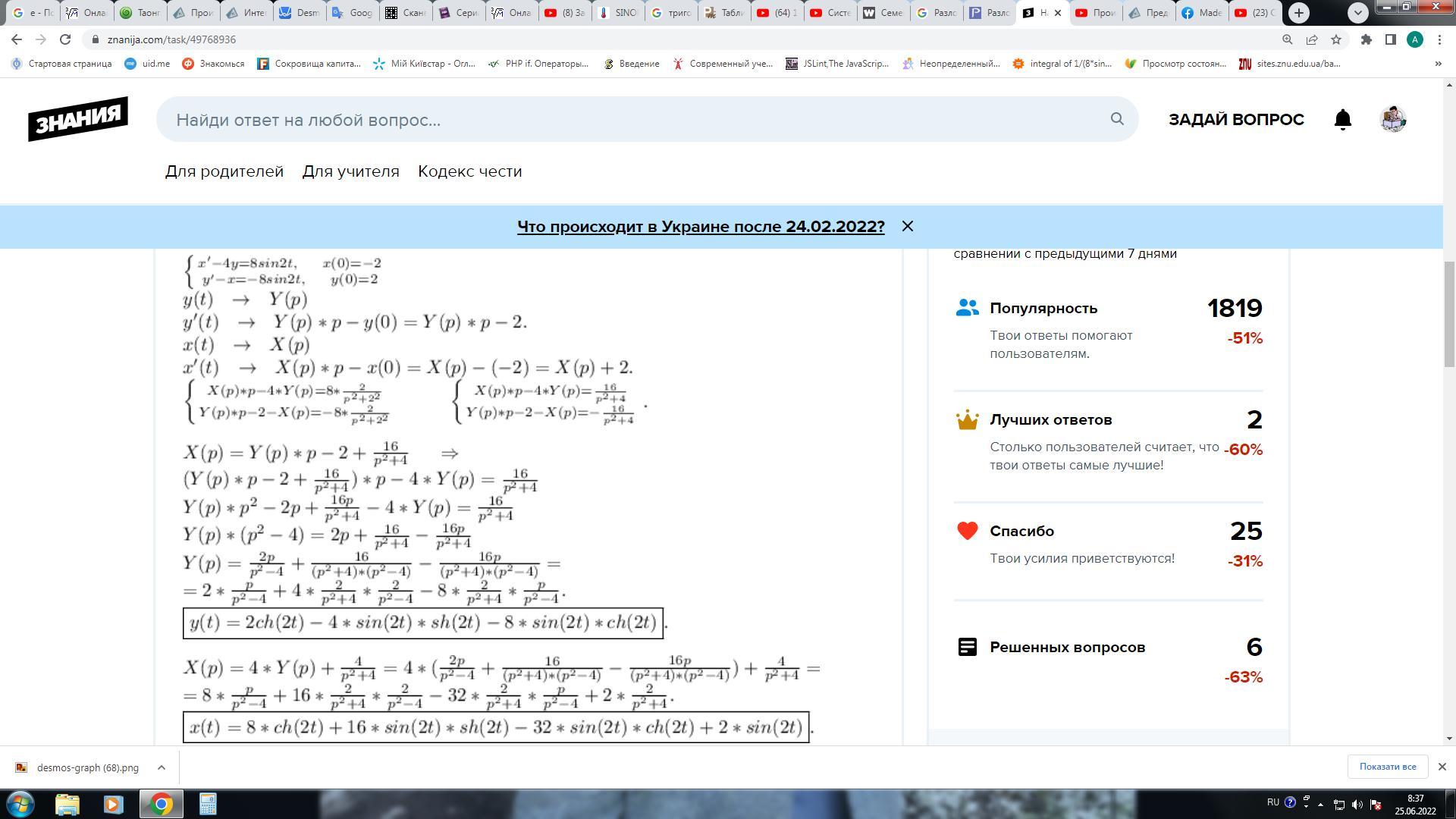
sangers1959:
Я решаю дальше.
Всё.
Похожие вопросы
Предмет: Английский язык,
автор: jans0999
Предмет: Русский язык,
автор: marisabel3056
Предмет: Русский язык,
автор: кирюха62
Предмет: Математика,
автор: tok12390