Предмет: Математика,
автор: Reideen
Задание приложено...
Приложения:
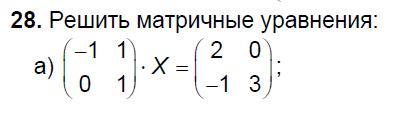
Ответы
Автор ответа:
2
Ответ:
Примечание:
Минором элемента определителя порядка
называется определитель порядка
, полученного из данного вычеркиванием
-й строки и
-го столбца и обозначается в виде
.
Алгебраическим дополнением элемента называют число:
Обратная матрица существует когда определитель исходной матрицы не равен нулю.
Обратная матрица:
Где:
- матрица из алгебраических дополнений элементов транспонированной матрицы
.
Пошаговое объяснение:
28.
а)
Пусть и
.
(при условии, что существует матрица обратная к матрице А)
Определитель матрицы А:
.
Так как , то
.
Алгебраические дополнения матрицы
Союзная матрица
Обратная матрица
----------------------------------------------------------------------
NNNLLL54:
неверно
Извините, но почему неверно?
после того, как вы исправили решение, стало верно
А, хорошо) Спасибо
Похожие вопросы
Предмет: Русский язык,
автор: koftina
Предмет: Английский язык,
автор: Angelina9080
Предмет: Қазақ тiлi,
автор: сания56216
Предмет: Математика,
автор: zoninmihail670
Предмет: Алгебра,
автор: anastasia090404