Предмет: Алгебра,
автор: chillaccount
30 баллов. Помоги разобраться в равенствах
Есть задание (1 скриншот) и есть его решение (2 скриншот).
Написано что из равенства ... следуют равернства... и перечеслины 3 равенства. Подскажите откуда они взялись? Как вообще догадаться до этого и откуда было мне знать что их еще и сложить потом нужно. Не понимаю почему в книге подобного не описывалось, да и в решении не особо подробно все описано, что и почему.
Приложения:
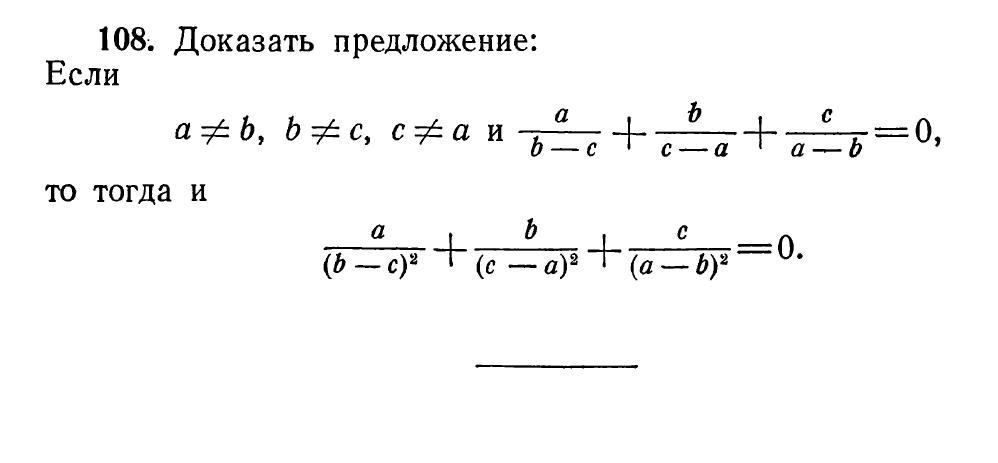

Ответы
Автор ответа:
1
Ответ:
Обозначим заданное выражение буквой А :
.
По условию А=0 , тогда и А * В = 0 * В = 0 , где В - любое другое
определённое выражение .
Похожие вопросы
Предмет: Русский язык,
автор: zalina110
Предмет: Окружающий мир,
автор: Матвейка0612
Предмет: Қазақ тiлi,
автор: NeZoX125152
Предмет: Биология,
автор: BORN221
Предмет: Литература,
автор: DmitriyOtvet