Предмет: Алгебра,
автор: danya053663
помогите решить уравнение
Приложения:
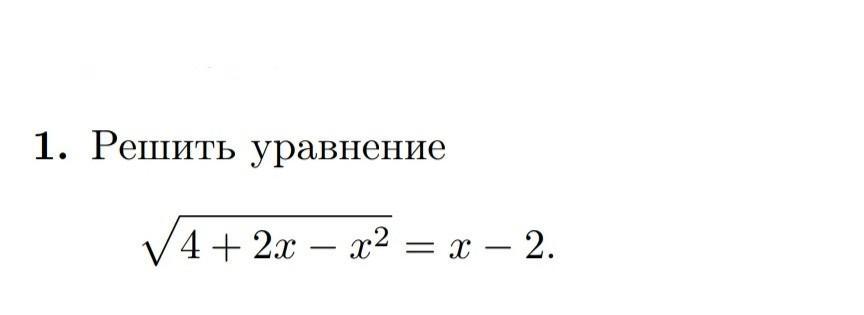
Ответы
Автор ответа:
1
Ответ:
х = 3
Объяснение:
Тогда имеем 2 решения —
х₁ = 0 3 - х₂ = 0
х₂ = 0 + 3 = 3.
Подставляем и проверяем —
Первое решение неверно, х ≠ 0.
Значит, уравнение имеет один корень — 3.
Похожие вопросы
Предмет: Окружающий мир,
автор: Enjoyboy
Предмет: Технология,
автор: nikafrank
Предмет: Русский язык,
автор: Осрдмадта
Предмет: Физика,
автор: Аноним
Предмет: Литература,
автор: Апах