Предмет: Математика,
автор: adrimoreno2020
решить всё, что подчёркнуто галочкой
Приложения:
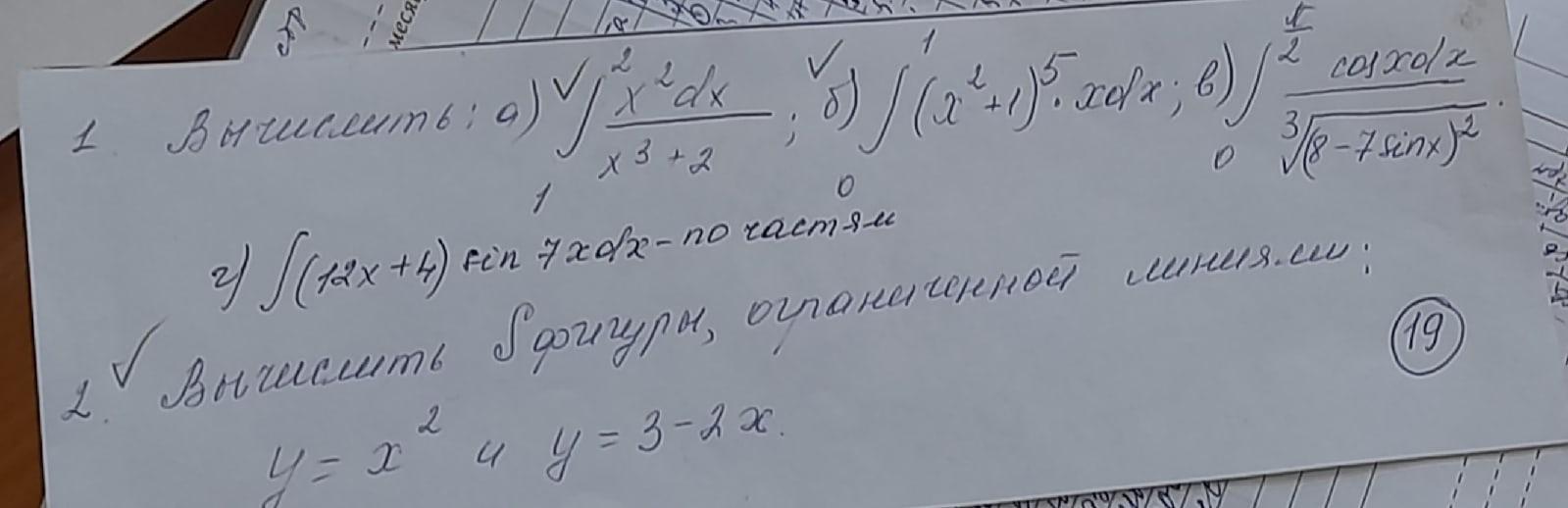
Ответы
Автор ответа:
3
Ответ:
1.
2. (ед)²
Пошаговое объяснение:
1. Вычислить :
Заметим что
Выйдет табличный интеграл
Находим определенный интеграл
Аналогично
Также выйдет табличный интеграл
Находим определенный интеграл
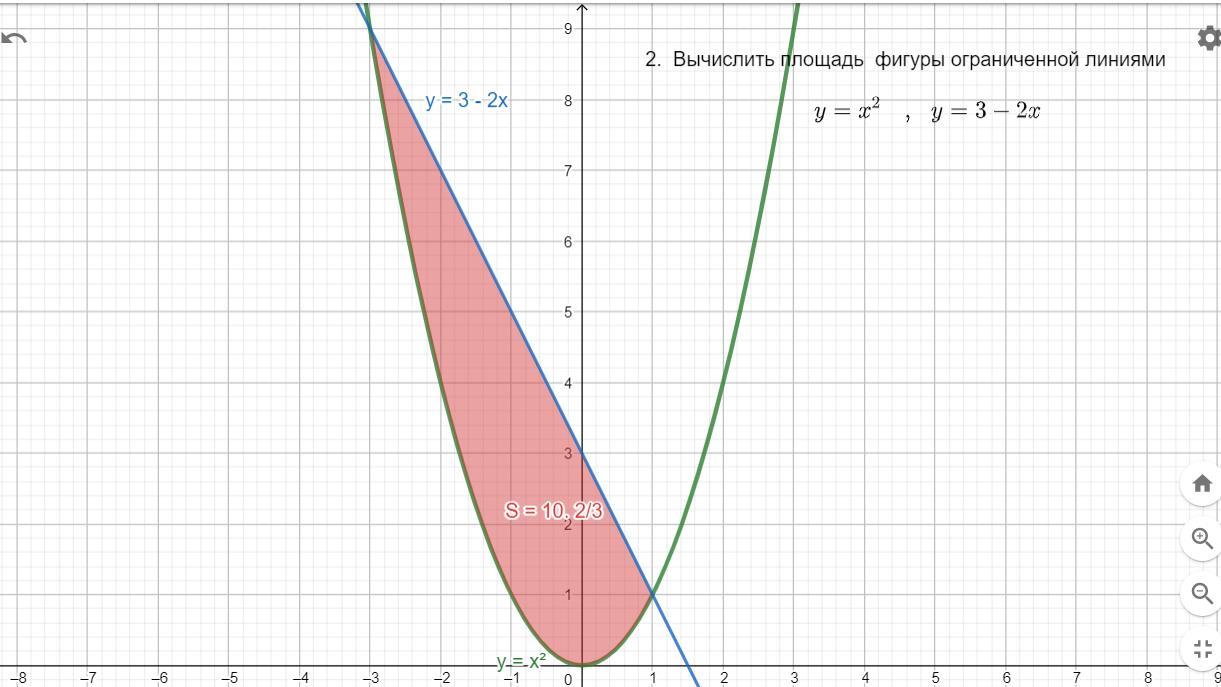
2. Вычислить площадь фигуры ограниченной линиями
Находим точки пересечений
Из промежутка ( -3 ; 1 ) берем любое число , к примеру x = 0
И подставляем в каждую функцию
1) y = x²
y = 0
2) y = 3 -2x
y = 3
Видно что вторая функция в данном промежутке больше первой , поэтому при нахождении площади от второй функции отнимем первую
Находим площадь
#SPJ1
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: незнайка946
Предмет: Английский язык,
автор: Masha2006111111
Предмет: Русский язык,
автор: 13253446
Предмет: Математика,
автор: denchik5389