Предмет: Математика,
автор: vanekvanc
решить все примеры с объяснением
Приложения:
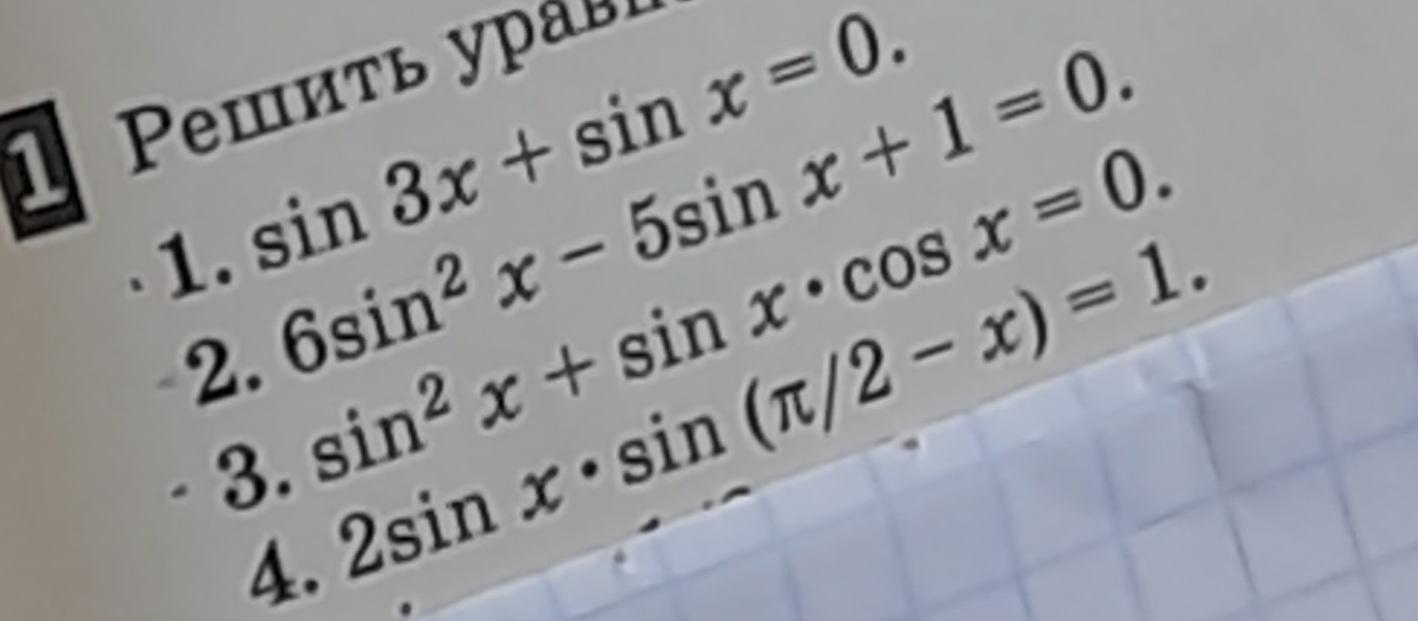
adrimoreno202:
12
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Решить уравнения:
Воспользуемся формулой
и получим:
Пусть , тогда уравнение принимает вид:
Возвращаясь к замене, получим
Воспользуемся формулами приведения и получим
По формуле синуса двойного угла
Тогда уравнение принимает вид:
#SPJ1
Похожие вопросы
Предмет: Русский язык,
автор: 13253446
Предмет: Русский язык,
автор: tkhabaev
Предмет: Окружающий мир,
автор: iradasalimova
Предмет: Алгебра,
автор: onoprienkor81
Предмет: Биология,
автор: Аноним