Предмет: Алгебра,
автор: MagicaeTalarium
Помогите, пожалуйста, решить.
Очень важен ход решения.
Приложения:
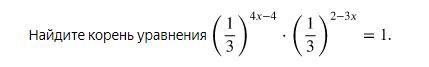
Ответы
Автор ответа:
3
Ответ:
решение смотри на фотографии
Приложения:
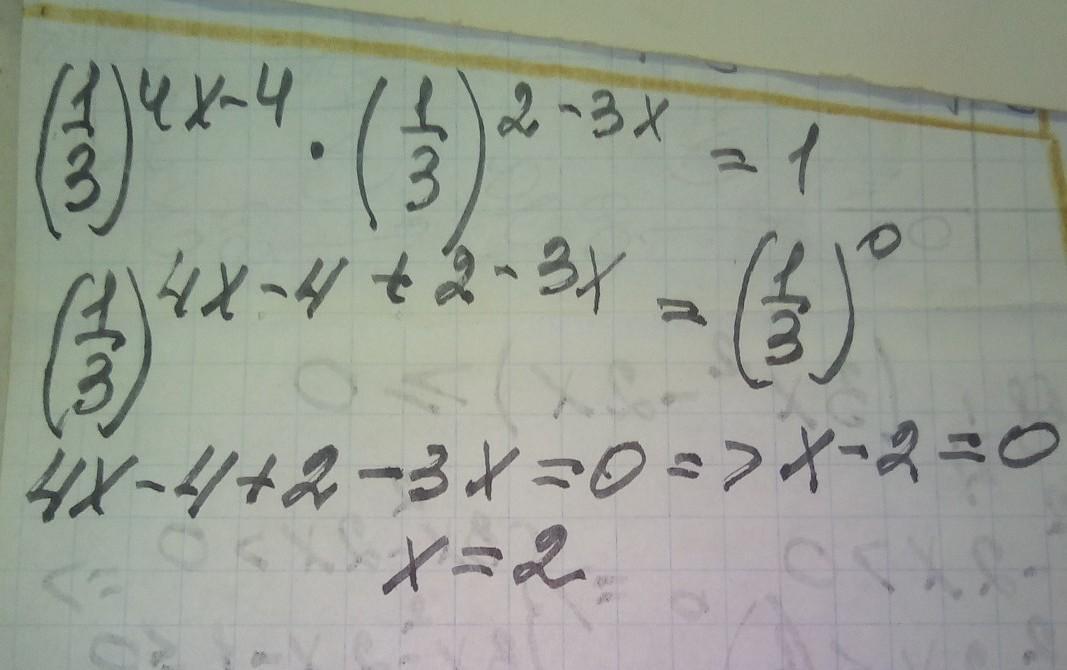
MagicaeTalarium:
Спасибо огромное, а то я не понимала, что с этой единицей делать, ещё и левую часть оказалось неправильно решала.
Автор ответа:
2
Решение.
Складываем показатели степеней.
Представим 1 как степень с основанием 1/3 .
Приравниваем показатели степеней .
Ответ: х=2 .
Похожие вопросы
Предмет: Английский язык,
автор: LoveKeti
Предмет: Русский язык,
автор: егорумный
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: matveugame