Как это сделать, пачаны и девчата?
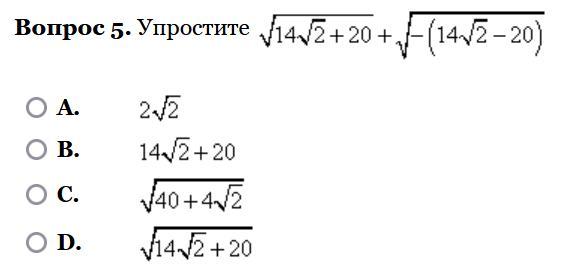
Ответы
Ответ: C) .
Формула сложного корня: .
Или можно обозначить и вычислить А²
Тогда .
Ответ: С. √(40+4√2)
Пошаговое объяснение:
Для решения этого задания достаточно двух формул школьной алгебры- квадрата суммы двух выражений и разности квадратов.
слегка преобразуем выражение.
пусть √(14√2+20)+√-(14√2-20)=√(20+14√2)+√(20-14√2)=х, тогда
х²=(√(20+14√2)+√(20-14√2))²
чтобы преобразовать правую часть, надо использовать школьную формулу (а+с)²=а²+2ас+с², где а =√(20+14√2), с=√(20-14√2)
х²=(√(20+14√2))²+2*(√(20+14√2))*(√(20-14√2))+(√(20-14√2))²=
20+14√2+2*√((20+14√2)*(20-14√2))+20-14√2=
40+2*√((20+14√2)*(20-14√2))
чтобы раскрыть подкоренное выражение , воспользуемся школьной формулой (а+с)*(а-с)=а²-с²
где а =√(20+14√2), с=√(20-14√2), получим
х²=40+2*√((20+14√2)*(20-14√2))=40+2*√((20²-(14√2)²)=
40+2*√(400-196*2)=40+2*√(400-392)=40+2*√8=40+2*2√2=40+4√2
зная х², найдем х.
х=√(40+4√2)
но х=√(14√2+20)+√-(14√2-20)
поэтому √(14√2+20)+√-(14√2-20)=√(40+4√2)
верный ответ С