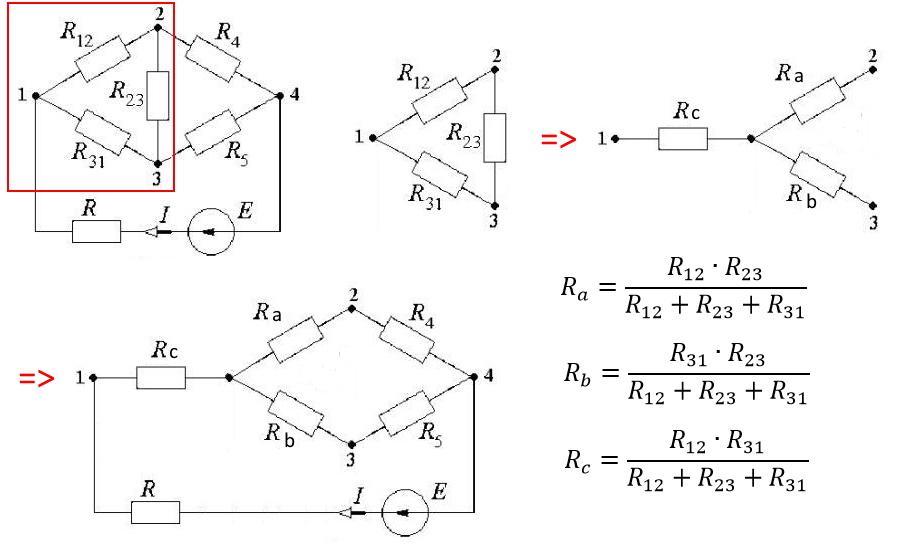
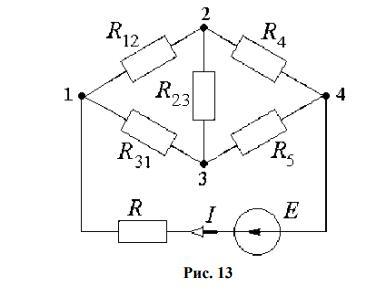
3адана мостова схема (рис. 13). R12 = 21 Ом; R23 = 30 Ом; R31 = 22 Ом; R4 =
8 Ом; R5 = 1,8 Ом; E = 160 В; R = 10 Ом. Розрахувати струм в опорі R.
Ответы
Ответ:
≈ 7 А
Объяснение:
3адана мостовая схема. R12 = 21 Ом; R23 = 30 Ом; R31 = 22 Ом; R4 = 8 Ом; R5 = 1.8 Ом; E = 160 В; R = 10 Ом.
Рассчитать ток в сопротивлении R.
-------
В мостовой схеме сопротивления R12, R23, R31 и R23, R4, R5 соединены по схеме "треугольник". Эквивалентное сопротивление этой схемы можно определить после замены одного из треугольников, например треугольника R12, R23, R31 звездой Rа, Rв, Rс (см приложение). Такая замена будет эквивалентной и не вызовет изменения токов всех остальных элементов цепи, если значения сопротивлений звезды рассчитать по следующим соотношениям:
Ra = R12*R23/(R12+R23+R31)
Rb = R31*R23/(R12+R23+R31)
Rc = R12*R31/(R12+R23+R31)
Подставляем:
Ra = 21*30/(21+30+22) = 630/73 ≈ 8.63 Ом
Rb = 22*30/(21+30+22) = 660/73 ≈ 9.04 Ом
Rc = 21*22/(21+30+22) = 462/73 ≈ 6.33 Ом
Теперь считаем эквивалентное сопротивление замещенной схемы.
Ra4 = Ra+R4 = 16.83
Rb5 = Rb+R5 = 10.84
Ra4b5 = Ra4*Rb5/(Ra4+Rb5) = 16.83*10.84/(16.83+10.84) ≈ 6.59 Ом
Сопротивление всей цепи равно:
Rэ = Ra4b5+Rc+R = 6.59+6.33+10 = 22.92 Ом
Ток в цепи (а он же и в сопротивлении R) равен:
I = U/Rэ = 160/22.92 ≈ 7 А