Предмет: Математика,
автор: Kirillka0709
Исследовать на экстремум функции
Приложения:
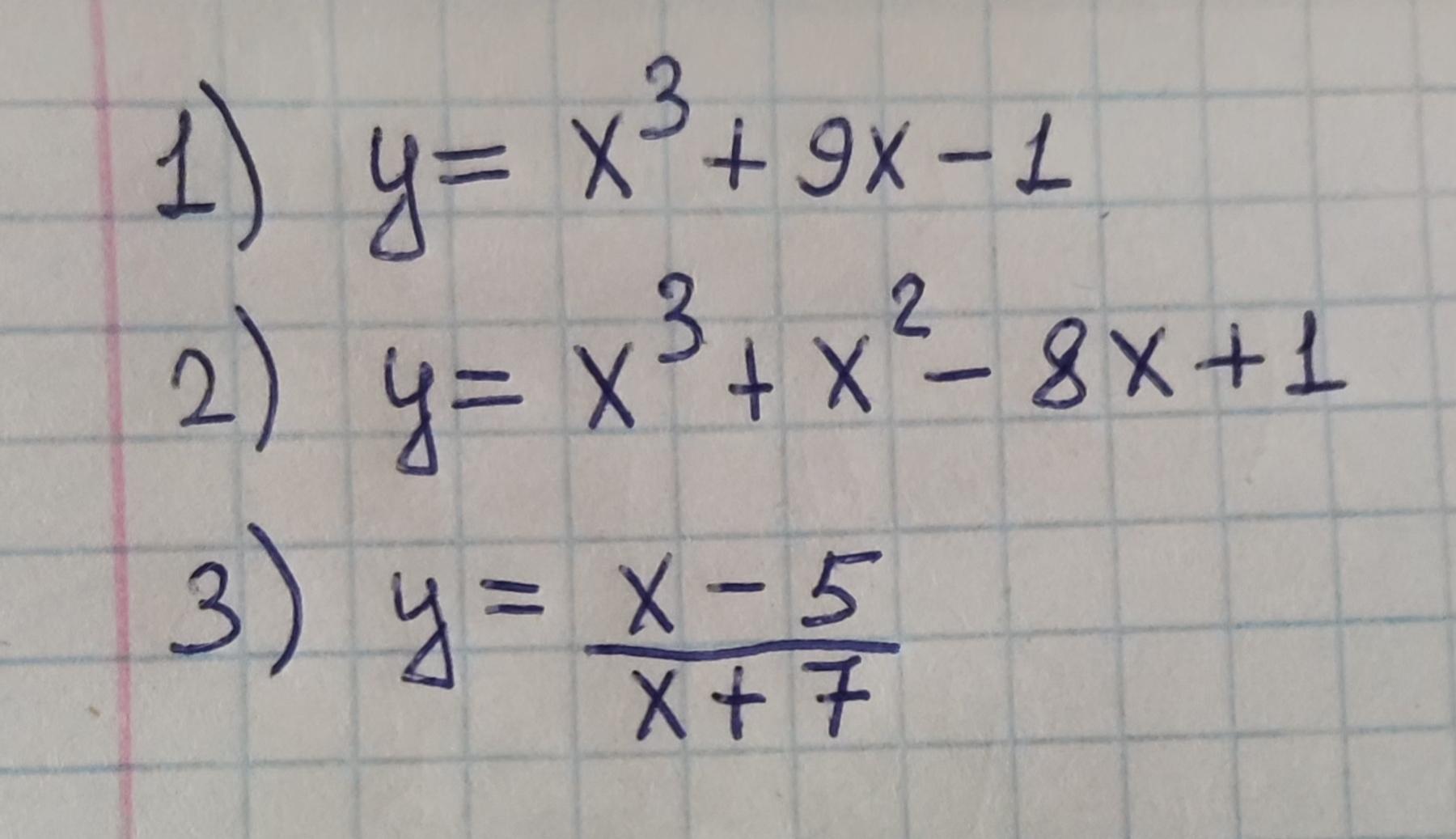
Ответы
Автор ответа:
1
Ответ:
1) экстремумов нет;
2) х min = 4/3; x max = -2;
3) экстремумов нет.
Пошаговое объяснение:
Исследовать на экстремум функции:
1) у = х³ + 9х - 1
2) у = х³ + х² - 8х + 1
3)
- Экстремум — максимальное или минимальное значение функции на заданном промежутке.
Для того, чтобы исследовать на экстремум функцию, надо:
- Найти производную, приравнять ее к нулю и найти корни.
- Отметить корни на числовой оси и определить знаки производной на промежутках.
- Если "+" - функция возрастает, если "-" - функция убывает.
- Если производная меняет знак с плюса на минус, то в данной точке наблюдается максимум, если с минуса на плюс, то в данной точке - минимум.
1) у = х³ + 9х - 1
y' = 3x² + 9
3x² ≥ 0 ⇒ 3x² + 9 > 0
Видим, что при любом значении х, производная положительна.
Значит функция возрастает на всем промежутке.
⇒ экстремумов нет.
2) у = х³ + х² - 8х + 1
y' = 3х² + 2х - 8
3х² + 2х - 8 = 0
Функция возрастает на промежутках: (-∞; -2]; [4/3; +∞).
Функция убывает на промежутке: [-2; 4/3]
х min = 4/3; x max = -2.
3)
Видим, что производная не может быть равна нулю.
В точке х = -7 производная не существует.
⇒ экстремумов нет.
#SPJ1
Похожие вопросы
Предмет: Українська мова,
автор: vikar4u4ka
Предмет: Русский язык,
автор: ritanesterenko1
Предмет: Другие предметы,
автор: Миха111111112
Предмет: Алгебра,
автор: polina128394