Question

Вычислить двойной интеграл xydxdy если область d ограничена линиями x = y^3, x = 0, y = 2
В методичке ответ 16.

Answer 1

Ответ:

16

Объяснение:

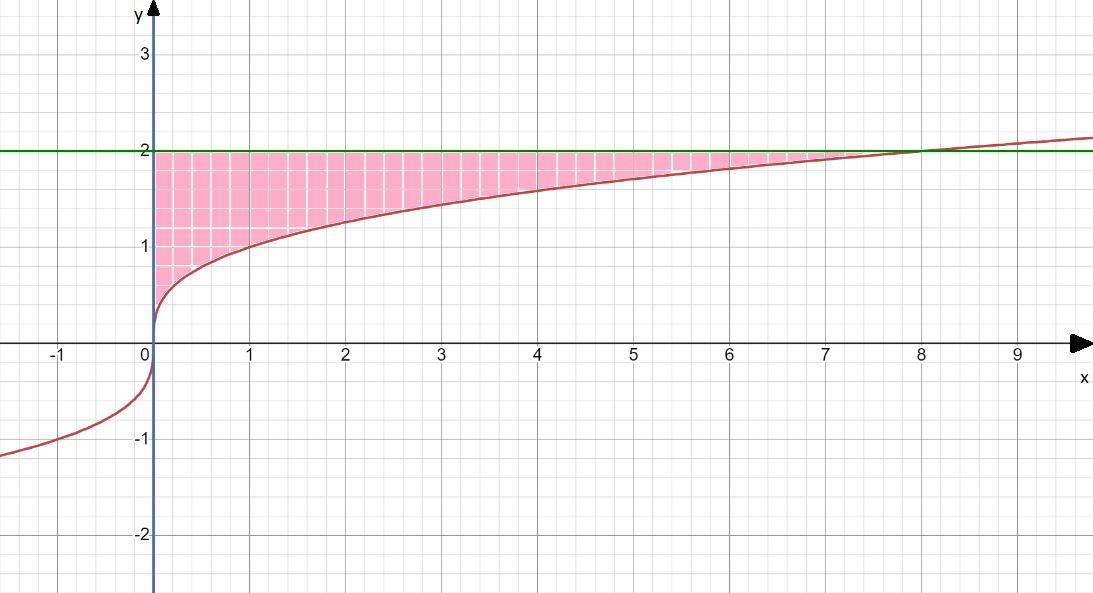
1) Нарисуем и выделим нужный участок(см. вложение)
2) Из рисунка мы видим, что
D: 0<y<2;
0<x<y³
3) Составим двойной интеграл
$\displaystyle \int\limits^2_0 {dy \int\limits^{y^3}_0 {xy} \,dx } =\int\limits^2_0 {y*\frac{x^2}{2}|^{y^3}_0 } \, dy =\int\limits^2_0 {\frac{y}{2}*((y^3)^2-0^2) } \, dy =\int\limits^2_0 {\frac{y^7}{2} } \, dy =\\=\frac{1}{2}*\frac{y^8}{8}|^2_0= \frac{1}{16}*(2^8-0^8) =\frac{2^8}{2^4} =2^{8-4}=2^4=16$
Также можно выразить у через х из первой функции, т. е.
x = y³ ⇔ y = ∛x, тогда
D: 0<х<8;
∛x<у<2
и двойной интеграл будет выглядеть как:
$\displaystyle \int\limits^8_0 {dx \int\limits^{2}_{\sqrt[3]{x} } {xy} \,dy }$
Конечный ответ будет тем же