Question

Допомоможіть вирішити завдання

Answer 1

Ответ:

1) $\vec a( 2;4;-2)$ и $\vec a( -2;-4;2)$

2) боковое ребро пирамиды равно 13 см.

Пошаговое объяснение:

1) Найти координаты вектора $\vec a(a;2a;-a)$, если его длина равна √24.

Длина вектора равна корню квадратному суммы квадратов координат вектора.

Значит,

$|\vec a|= \sqrt{a^{2}+(2a)^{2} +(-a)^{2} }$

По условию длина вектора равна √24. Тогда получим уравнение

$\sqrt{a^{2}+(2a)^{2} +(-a)^{2} }=\sqrt{24}$

Возведем обе части в квадрат и получим:

$a^{2} +4a^{2} +a^{2} =24;\\6a^{2} =24;\\a^{2} =24:6;\\a^{2}=4;\\a=\pm2$

При а=2 вектор имеет координаты $\vec a( 2;4;-2)$

При а= -2 вектор имеет координаты $\vec a( -2;-4;2)$

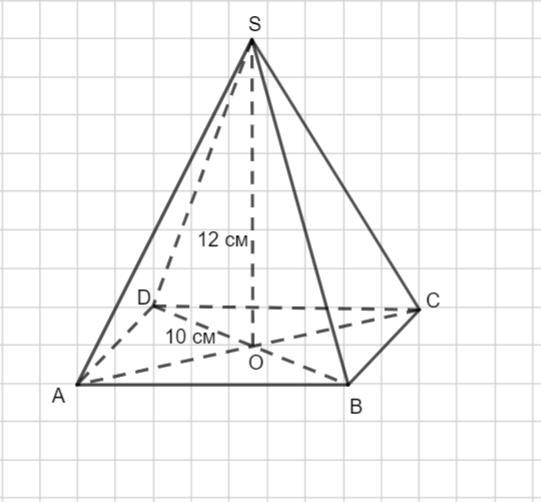
2) В основании пирамиды лежит прямоугольник, диагональ которого равна 10 см. Все боковые ребра равны. Найти боковое ребро пирамиды, если  высота пирамиды равна 12 см.

Пусть дана пирамида SABCD. Основание пирамиды квадрат ABCD. Его диагонали АС =BD = 10 см .

Все боковые ребра равны, то есть AS=BS=CS=DS.

Тогда Δ SOA=ΔSOB=ΔSOC=ΔSOD по гипотенузе и катету

( катет SO-общий, а гипотенузы AS=BS=CS=DS равны по условию)

Из равенства треугольников следует, что

AO=BO=CO=DO и точка О - точка пересечения диагоналей. Диагонали точкой пересечения делятся пополам.

AO=BO=CO=DO =10:2=5 см.

Рассмотрим  Δ АОS - прямоугольный. Найдем боковое ребро по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$AS^{2} =AO^{2} +OS^{2} ;\\AS= \sqrt{AO^{2} +OS^{2} } } ;\\AS= \sqrt{5^{2}+12^{2} } =\sqrt{25+144} =\sqrt{169} =13$ см.

#SPJ1