Question

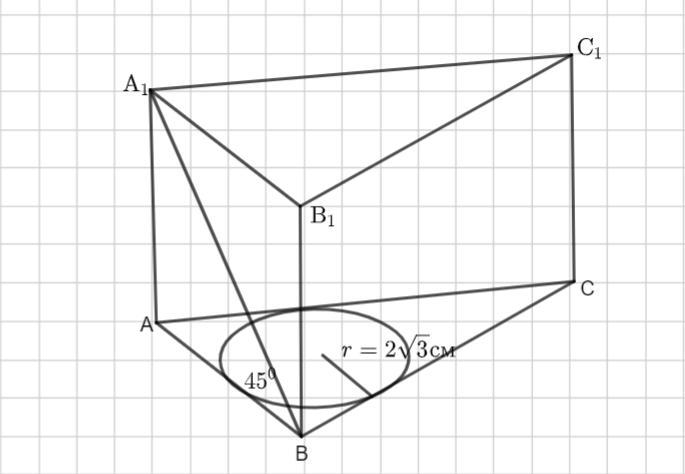
В правильной треугольной призме радиус окружности, вписанной
в основание, равен 2√3 см. Диагональ боковой грани образует с
плоскостью основания угол 450
. Найти площадь боковой
поверхности призмы.

Answer 1

Ответ:

Площадь боковой поверхности призмы  равна 432 см².

Пошаговое объяснение:

В правильной треугольной призме радиус окружности вписанной в основание, равен  2√3 см. Диагональ боковой грани образует с плоскостью основания угол 45°. Найти площадь боковой поверхности призмы.

Пусть дана правильная призма $ABCA_{1} B_{1} C_{1}$ . Тогда Δ АВС - правильный и по условию известен радиус вписанной окружности.

Радиус окружности, вписанной в правильный треугольник определяется по формуле

$r=\dfrac{a}{2\sqrt{2} } ,$

где а - сторона треугольника.

Тогда

$a=2r\sqrt{3}$

Найдем сторону треугольника АВС

$AB=AC=BC=2\cdot 2\sqrt{3} \cdot \sqrt{3} =4\cdot3=12$ cм.

Рассмотрим Δ$A_{1} AB$ - прямоугольный, если ∠$A_{1} BA=45^{0}$, то

∠$AA_{1} B=45^{0}$ ( так как сумма острых углов прямоугольного треугольника равна 90°). Тогда Δ$A_{1} AB$ - равнобедренный ( два угла равны) и $A_{1} A=AB =12$ см. Значит, высота призмы равна 12 см.

Площадь боковой поверхности правильной призмы равна произведению периметра основания на высоту.

Периметр правильного треугольника вычисляется по формуле

$P=3a,$ где а - сторона треугольника

$P=3\cdot12 =36$ cм.

Площадь боковой поверхности правильной призмы будет равна

$S= 36\cdot 12=432$ см².

#SPJ1