Предмет: Математика,
автор: zlatabelkacom
Помогите, пожалуйста, решить данную задачу
Приложения:
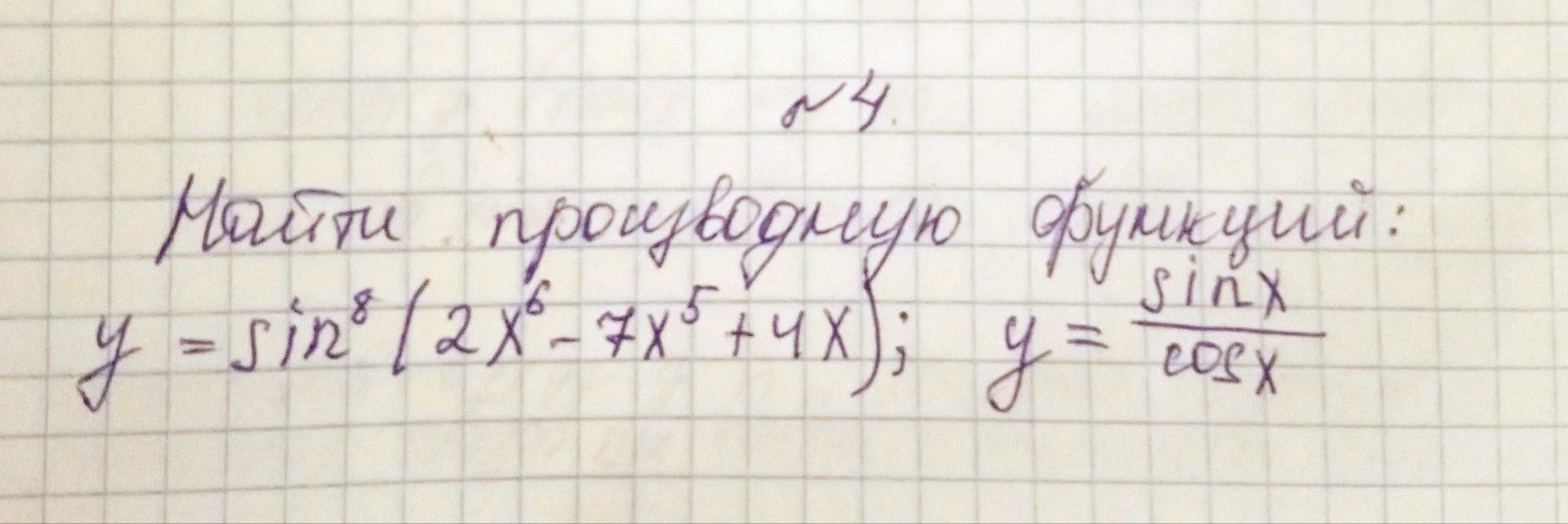
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Найти производную функции
1)
Воспользуемся правилом нахождения производной сложной функции и следующими формулами
( постоянный множитель выносится за знак производной)
Тогда получим
2)
Воспользуемся правилом нахождения производной частного и получим:
Конечно, можно было данную функцию представит в виде тангенса и найти производную
#SPJ1
Похожие вопросы
Предмет: Русский язык,
автор: kamillakaya07
Предмет: Другие предметы,
автор: сонька145
Предмет: Английский язык,
автор: Skinner56825
Предмет: Русский язык,
автор: nikitosikk8238
Предмет: Геометрия,
автор: lamiya84