Предмет: Геометрия,
автор: selenagom2438
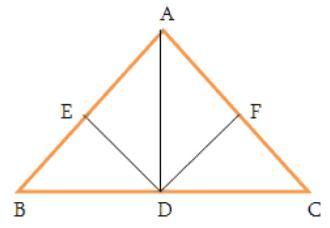
В треугольнике АВС медианы АВ и АС пересекаются в точке D
1) доказать что точка D середина ВС
2) доказать что <А= <В -<С
Приложения:
Ответы
Автор ответа:
2
Ответ:
1) В треугольнике ЕВD по теорему Пифагора ВD²=ЕD²+ВЕ²
В треугольнике ЕАD по теорему Пифагора АD²=ЕD²+АЕ²
Поскольку ЕD медиана стороны АВ ⇒ ЕА=ЕВ
так как ЕА=ЕВ ⇒ ВD²=АD²⇒ ВD=АD
В треугольнике FDС по теорему Пифагора
СD²=FD²+FС²
В треугольнике FDА по теорему Пифагора
АD²=DF²+АF²
FD медиана стороны АС ⇒
СD²=АD²⇒
СD=АD
получается что ВD=АD СD=АD
⇒ ВD=DС
2) Поскольку треугольник DАС равнобедренный ⇔ АD=СD ⇒
∠DАС=∠С
Поскольку треугольник DАВ равнобедренный ⇔ АD=ВD ⇒
∠DАВ=∠В
очевидно что ∠А=∠В+∠С
selenagom2438:
пасиб
Похожие вопросы
Предмет: Русский язык,
автор: Aleks8350
Предмет: Технология,
автор: Краснаям
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: Gyunay14
Предмет: Математика,
автор: bratzyn