Предмет: Алгебра,
автор: ozodbekk
быстро пж решите без калькулятора оба
Приложения:

Ответы
Автор ответа:
1
Ответ:
а)
Объединим числитель с помощью фориулы умножения корней:
Воспользуемся формулой разности квадратов:
Деление корней:
б)
Автор ответа:
1
Ответ:
........
Объяснение:
Приложения:
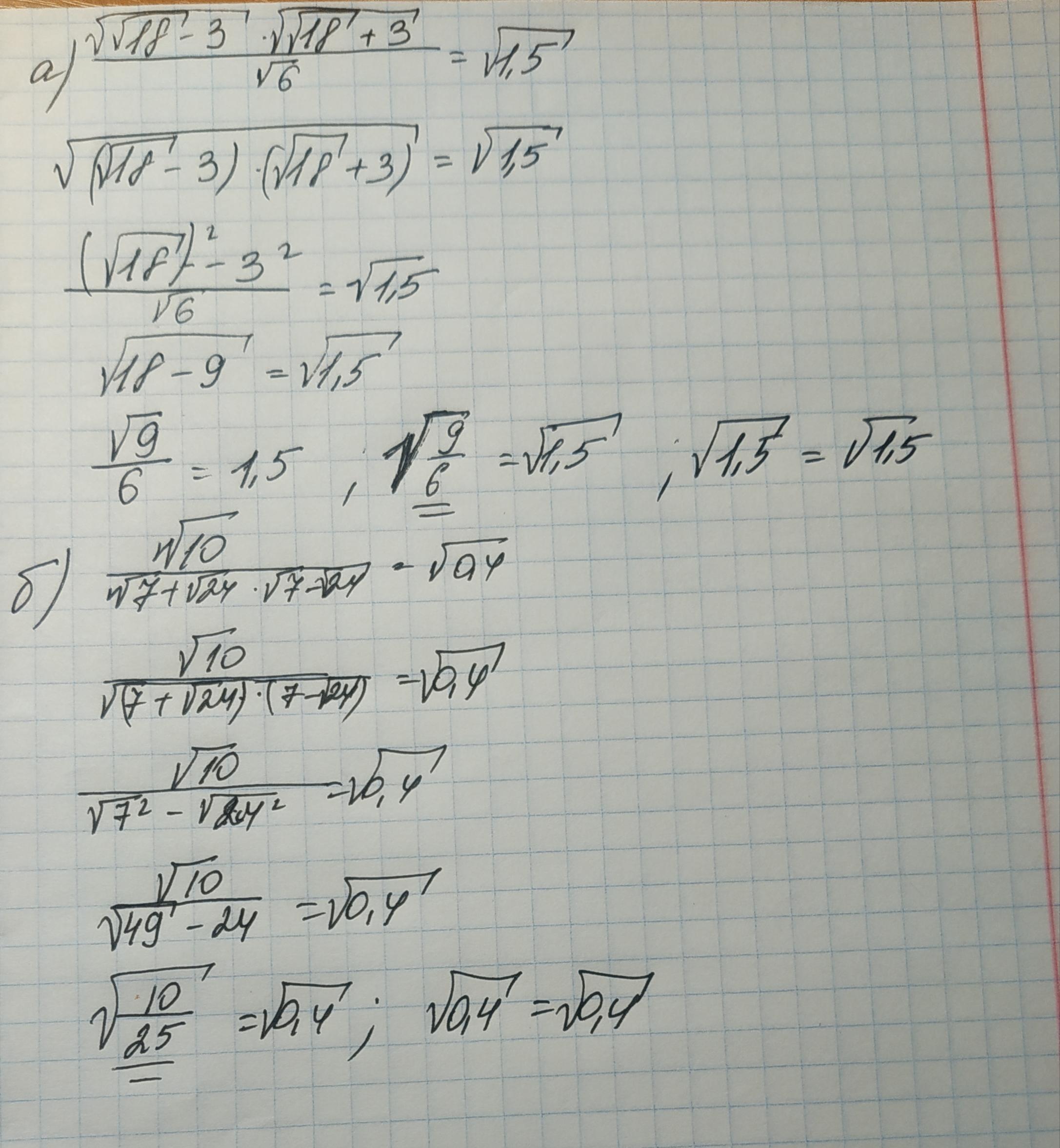
Похожие вопросы
Предмет: Українська мова,
автор: Roma5465
Предмет: Английский язык,
автор: чепешка
Предмет: Русский язык,
автор: Annaohnaleva
Предмет: География,
автор: zazak12370
Предмет: ОБЖ,
автор: Аноним