Предмет: Алгебра,
автор: Аноним
Здравствуйте , помогите решить высшая математика
Приложения:
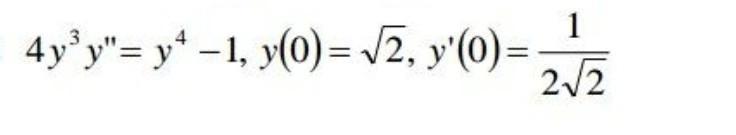
Ответы
Автор ответа:
3
Ответ:
a) В дифф. ур. не присутствует переменная х , поэтому делаем
замену .
Подставим начальные условия в :
.
Определим, какой знак надо выбрать из начальных условий.
В левой части , в правой части
. Поэтому выбираем знак плюс .
Подставляем начальные условия : .
Подставим 0 вместо константы, получим
Выбираем знак из начальных условий.
В левой части , в правой части выражение будет равняться 2, если перед функцией
взять плюс, так как
.
Частное решение д.у. 2 порядка, допускающего понижение
порядка, имеет вид: .
Опять выбираем знак с учётом начальных условий: .
solka0000:
допоможіть , з диференційним рівнянням , будь ласка
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: яСвелана
Предмет: Қазақ тiлi,
автор: oleg7355608
Предмет: Геометрия,
автор: Dmandreev003
Предмет: Алгебра,
автор: Аноним