Найдите промежутки возрастания функции и ее точки экстремума.
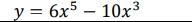
Ответы
Ответ:
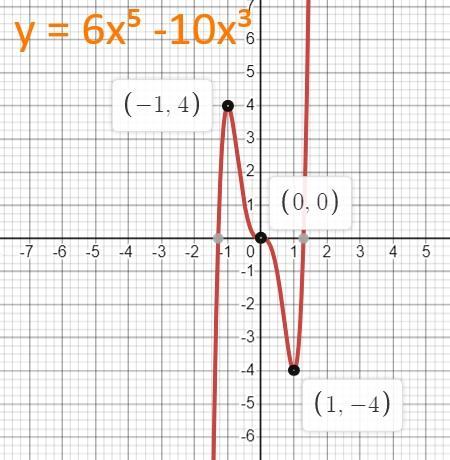
функция имеет две точки экстремума:
x₂ = -1 точка максимума функции;
x₁ = 1 точка минимума функции.
функция возрастает на промежутках (-∞ ;-1] и [1; +∞)
Объяснение:
y = 6x⁵ -10x³
1) точки экстремума.
Найдем критические точки.
y'(x₀) = 0 - это необходимое условие экстремума функции.
y'(x) = (6x⁵ -10x³)' = 30x⁴ -30x² = 30x²(x² -1)
x₁ = 1
x₂ = -1
x₃ = 0
Однако, пока не понятно, есть в этих точках экcтремум и какой - минимум или максимум.
Используем достаточное условие экстремума функции.
Вторая производная
y''( 30x⁴ -30x²)' = 120x³-60x
Исследуем знак второй производной в критических точках
y''(0) = 0 = 0 - значит точка x₃ = 0 точка перегиба функции.
y''(-1) = -60 < 0 - значит точка x₂ = -1 точка максимума функции.
y''(1) = 60 > 0 - значит точка x₁ = 1 точка минимума функции.
Таким образом, функция имеет две точки экстремума:
x₂ = -1 точка максимума функции;
x₁ = 1 точка минимума функции.
2) промежутки возрастания.
Учитывая найденные в первом пункте критические точки, мы имеем 4 интервала для изучения.
(-∞ ;-1] [-1; 0] [0; 1] [1; +∞)
Рассмотрим поведение первой производной на каждом интервале.
(-∞ ;-1]
y'(-2) = 360 > 0 - функция возрастает;
[-1; 0]
y'(-0,5) = -5,625 < 0 - функция убывает;
[0; 1]
y'(0,5) = -5,625 < 0 - функция убывает;
[1; +∞)
y'(2) = 360 > 0 - функция возрастает;
Таким образом, функция возрастает на промежутках (-∞ ;-1] и [1; +∞)
#SPJ1