Question

1) Знайти похідну функції
2) Дослідити функцію і намалювати графік
якщо можна напишіть це налисточку, буду вдячний

Answer 1

Ответ:

1) Производная функции  $\displaystyle y=sin^4\;\frac{x}{3}$ равна:

$\displaystyle y'=\frac{4}{3} sin^3\;\frac{x}{3} \cdot{cos\;\frac{x}{3}$

2) Исследовали функцию:

1. ОДЗ: х ∈ R;

2. Функция не является четной или нечетной, то есть общего вида.

3. а) х = 0 ⇒ у = 0;

б) у = 0 ⇒ х = 0;   х = 3.

4. Функция непрерывна, асимптот нет.

5. Функция возрастает на промежутках: [0; 2];

функция убывает на промежутках: (-∞; 0]; [2; +∞);

х max = 2,   x min = 0.

6. функция вогнута на промежутке (-∞; 1];

функция выпукла на промежутке [1; +∞).

х перегиба = 1.

Пошаговое объяснение:

1) Найти производную функции   $\displaystyle y=sin^4\;\frac{x}{3}$.

Используем формулы производных сложных функций:

$\displaystyle \boxed {(u^n)'=nu^{n-1}u'},\;\;\;\boxed {(sin\;u)'=cos\;u\cdot{u'}}$

Найдем производную:

$\displaystyle y'=\left(sin^4\;\frac{x}{3} \right)'=4sin^3\;\frac{x}{3}\cdot{\left(sin\;\frac{x}{3}\right)' } =\\\\=4sin^3\;\frac{x}{3} \cdot{cos\;\frac{x}{3}\cdot\left(\frac{x}{3}\right)' }=\\\\=4sin^3\;\frac{x}{3} \cdot{cos\;\frac{x}{3}\cdot\frac{1}{3} }=\frac{4}{3} sin^3\;\frac{x}{3} \cdot{cos\;\frac{x}{3}$

2) Исследовать функцию и построить график:

y = 3x² - x³

1. ОДЗ: х ∈ R.

2. Четность, нечетность.

Если f(-x) = f(x), то функция четная, если f(-x) = -f(x) - нечетная.

f(-x) = 3(-x)² - (-x)³ = 3x² + x³

f(-x) ≠ f(x) ≠ -f(x) ⇒ функция не является четной или нечетной, то есть общего вида.

3. Пересечение с осями.

а) х = 0 ⇒ у = 0

б) у = 0 ⇒ х²(3 - х) = 0

х = 0;   х = 3

4. Асимптоты.

Функция непрерывна, асимптот нет.

5. Возрастание, убывание, экстремумы.

Найдем производную, приравняем к нулю и найдем корни. Отметим их на числовой оси и определим знаки производной на промежутках.

• Если "+" - функция возрастает, если "-" - функция убывает.

у' = 3 · 2x - 3x² = 6x - 3x² = 3x (2 - x)

3x (2 - x) = 0

x = 0;   x = 2.

$---[0]+++[2]---$

⇒ Функция возрастает на промежутках: [0; 2];

функция убывает на промежутках: (-∞; 0]; [2; +∞)

• Если производная меняет знак с плюса на минус, то в данной точке наблюдается максимум, если с минуса на плюс, то в данной точке  - минимум.

⇒ х max = 2,   x min = 0.

y(2) = 4,   y(0) = 0

6. Выпуклость, вогнутость.

Найдем производную второго порядка, приравняем к нулю и найдем корни. Отметим их на числовой оси и определим знаки второй производной на промежутках.

• Если производная второго порядка положительна, функция вогнута, если отрицательна - выпукла.

y'' = 6 - 6x = 6(1 - x)

6(1 - x) = 0

x = 1

$+++[1]---$

⇒ Функция вогнута на промежутке (-∞; 1];

функция выпукла на промежутке [1; +∞).

х перегиба = 1;

у(1) = 2

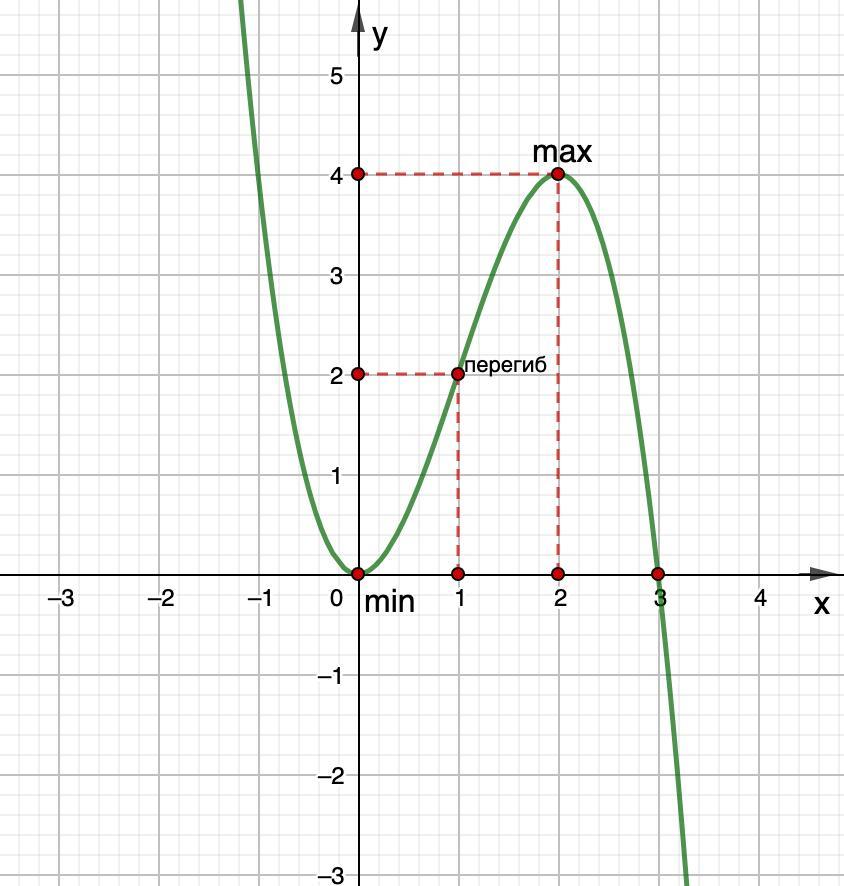
Строим график.

#SPJ1