Question

Срочно нужно, с рисунком
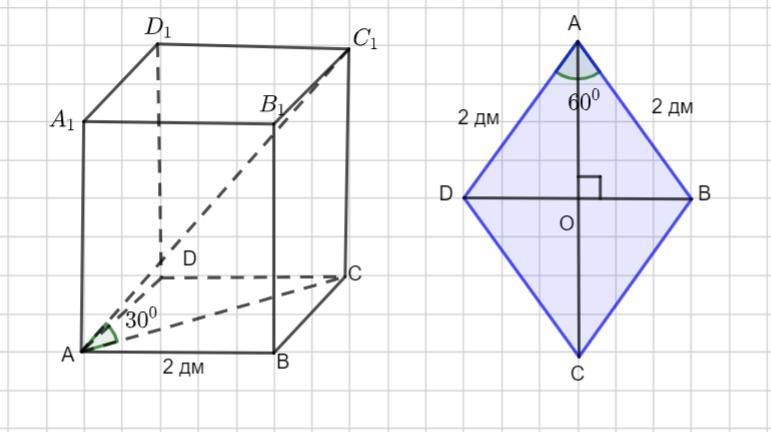
Основанием прямого параллелепипеда является ромб с острым
углом 600
и стороной 2 дм. Большая диагональ параллелепипеда
наклонена к плоскости основания под углом 300
Найти площадь боковой поверхности параллелепипеда.

Answer 1

Ответ:

Площадь боковой поверхности параллелепипеда 16дм²

Объяснение:

Основанием прямого параллелепипеда является ромб со стороной 2 дм и острым углом 60°. Большая диагональ параллелепипеда наклонена к плоскости основания под углом 30°. Найти площадь боковой поверхности параллелепипеда.

Площадь боковой поверхности параллелепипеда определяется как произведение периметра основания на высоту параллелепипеда.

Найдем периметр ромба АВСD.

$P=4a,$

где а - сторона ромба

$P=4\cdot 2 =8$ дм.

Найдем высоту параллелепипеда.

Найдем большую диагональ ромба. Диагонали ромба пересекаются под прямым углом, точкой пересечения делятся пополам и диагонали ромба являются биссектрисами углов.

Тогда ∠DAO=∠BAO=60°:2=30°.

Рассмотрим ΔАОВ - прямоугольный.

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

$cos 30^{0} =\dfrac{AO}{AB} ;\\\\\dfrac{\sqrt{3} }{2} =\dfrac{AO}{2} ;\\\\AO= \sqrt{3}$дм.

Тогда АС =2√3 дм.

Рассмотрим Δ$ACC_{1}$ - прямоугольный.

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

$tg30^{0} =\dfrac{CC_{1} }{AC} ;\\\\\dfrac{1}{\sqrt{3} } =\dfrac{CC_{1} }{2\sqrt{3} };\\\\CC_{1} =\dfrac{2\sqrt{3} }{\sqrt{3} } =2$

Тогда высота параллелепипеда равна 2 дм.

Найдем площадь боковой поверхности параллелепипеда

$S =8\cdot 2 =16$ дм².

#SPJ1