Предмет: Математика,
автор: murlasik
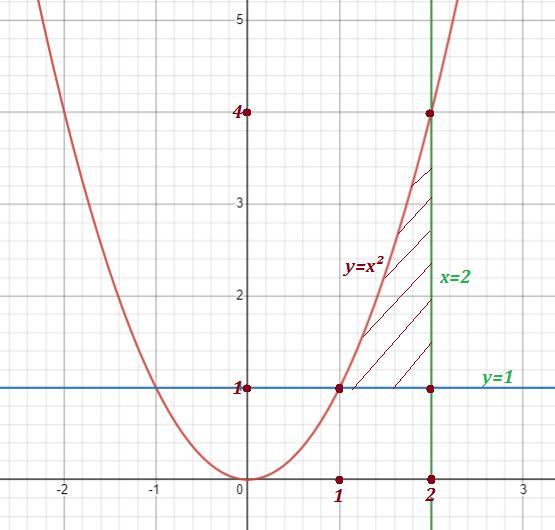
Обчислити об’єм тіл, утворених обертанням фігур, обмежених графіками
функцій. (вісь обертання Ох)
y=x^2; y=1; x=2.
Ответы
Автор ответа:
2
Ответ:
Точки пересечения параболы y=x² и прямых:
Объём тела, образованного вращением заданной области вокруг оси ОХ равен
Ответ: (куб.ед.) .
Приложения:
pushpull:
там не площадь нужна, а объем
спасибо
Похожие вопросы
Предмет: Қазақ тiлi,
автор: TheIgroman
Предмет: Другие предметы,
автор: Alina2101
Предмет: Русский язык,
автор: Александр5671
Предмет: Алгебра,
автор: kest10
Предмет: Геометрия,
автор: fifaworld55