20 Баллов. Как разложить многочлен на множители?
Дано тождество и нужно доказать его. В книге также дано решение, но оно совсем непонятно. В чатности непонятно то что выделено красными рамками на скриншоте. Подскажите что и как раскладывается после замены на х y z
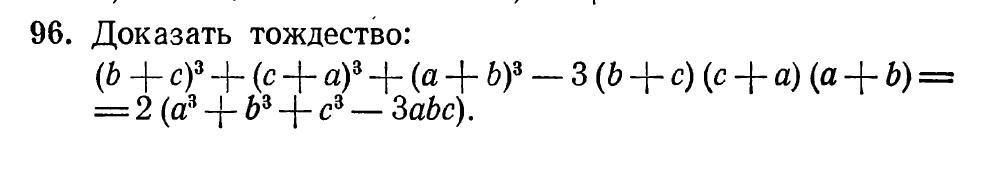
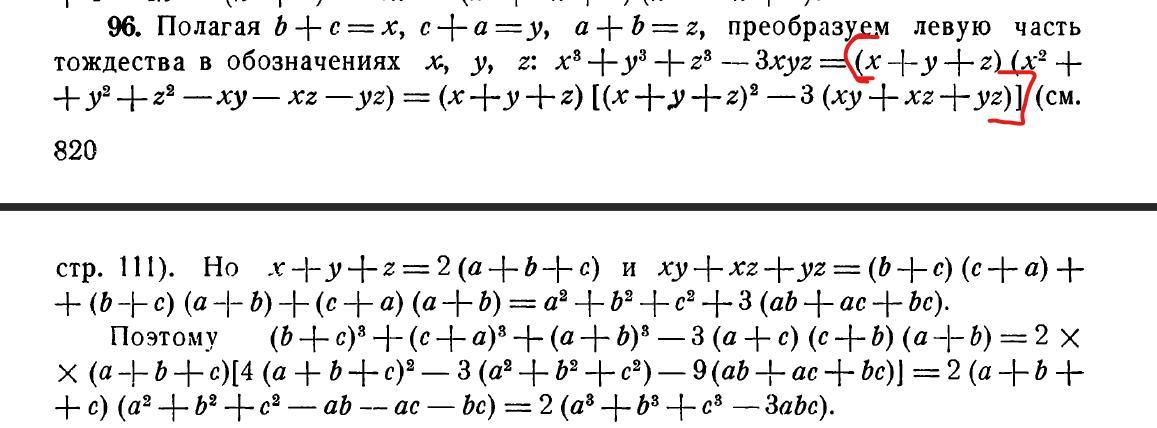
Ответы
Ответ:
(см. объяснение)
Объяснение:
Я так понимаю, что задающему вопрос непонятно, как прийти к формуле:
Я предлагаю подход, описанный ниже.
Запишем такое кубическое уравнение, корнями которого являются числа a, b, с:
Соответственно подставляем x=a:
Подставляем x=b:
Подставляем x=c:
Теперь складываем 3 строки, записанные выше:
Тогда верно, что:
И соответственно выносим a+b+c за скобки:
Получили известную в узких кругах формулу.
Теперь автор просит рассмотреть преобразования во второй скобке правой части равенства, записанного выше:
Здесь стоит вспомнить очень известную формулу:
Тогда все станет более чем понятно.
Дальнейшие комментарии по этому пункту не считаю необходимыми.
Задание выполнено!
Комментарий:
В приведенной Вами фотографии доказательства пояснено, что в случае вопроса по указанному переходу разумно обратиться к странице 111 учебника/задачника, предлагающего данного решение. Полагая, что Вы сделали это перед тем, как задать вопрос, уточню, что правильнее было бы указать на проблему в осознании того, что написано на странице 111 для получения более детального объяснения в областях, наиболее трудно дающихся Вам в осознании и осмыслении.