Question

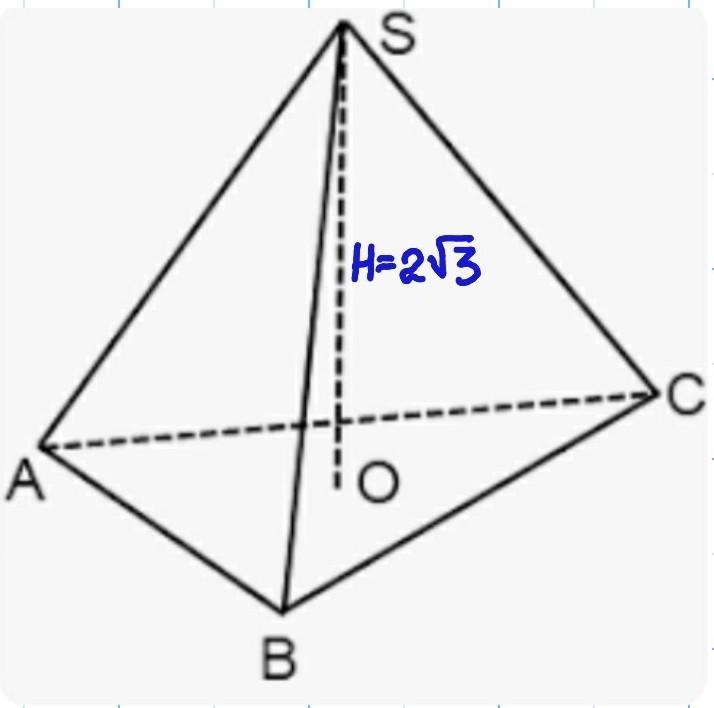
Вычислите длину стороны основания правильной треугольной пирамиды
с объемом 2 см3 и высотой 2√3см.
С решением и чертежом,пожалуйста!

Answer 1

Ответ:

Сторона основания правильной треугольной пирамиды равна 2 см

Объяснение:

Объем правильной треугольной пирамиды равен 2 см³, высота - 2√3см. Надо вычислить длину стороны основания.

• Правильная треугольная пирамида — это пирамида с правильным треугольником в основании (грани же должны быть равнобедренными треугольниками).

Объем пирамиды находится по формуле:

V =⅓•Sосн•Н,

где Sосн - площадь основания, Н - высота пирамиды.

так как по условию V=2 см³, Н=2√3см, то найдём Sосн:

⅓•Sосн•2√3=2

Sосн = 3/√3 = √3 см²

Площадь правильного треугольника находится по формуле:

$S = \dfrac{ \sqrt{3} }{4} {a}^{2}$

Подставим известные величины:

$\dfrac{ \sqrt{3} }{4} {a}^{2} = \sqrt{3}$

а²=4

а=2 см (-2 не подходит)

Ответ: Сторона основания правильной треугольной пирамиды равна 2 см

#SPJ1