Предмет: Алгебра,
автор: 19219291921921
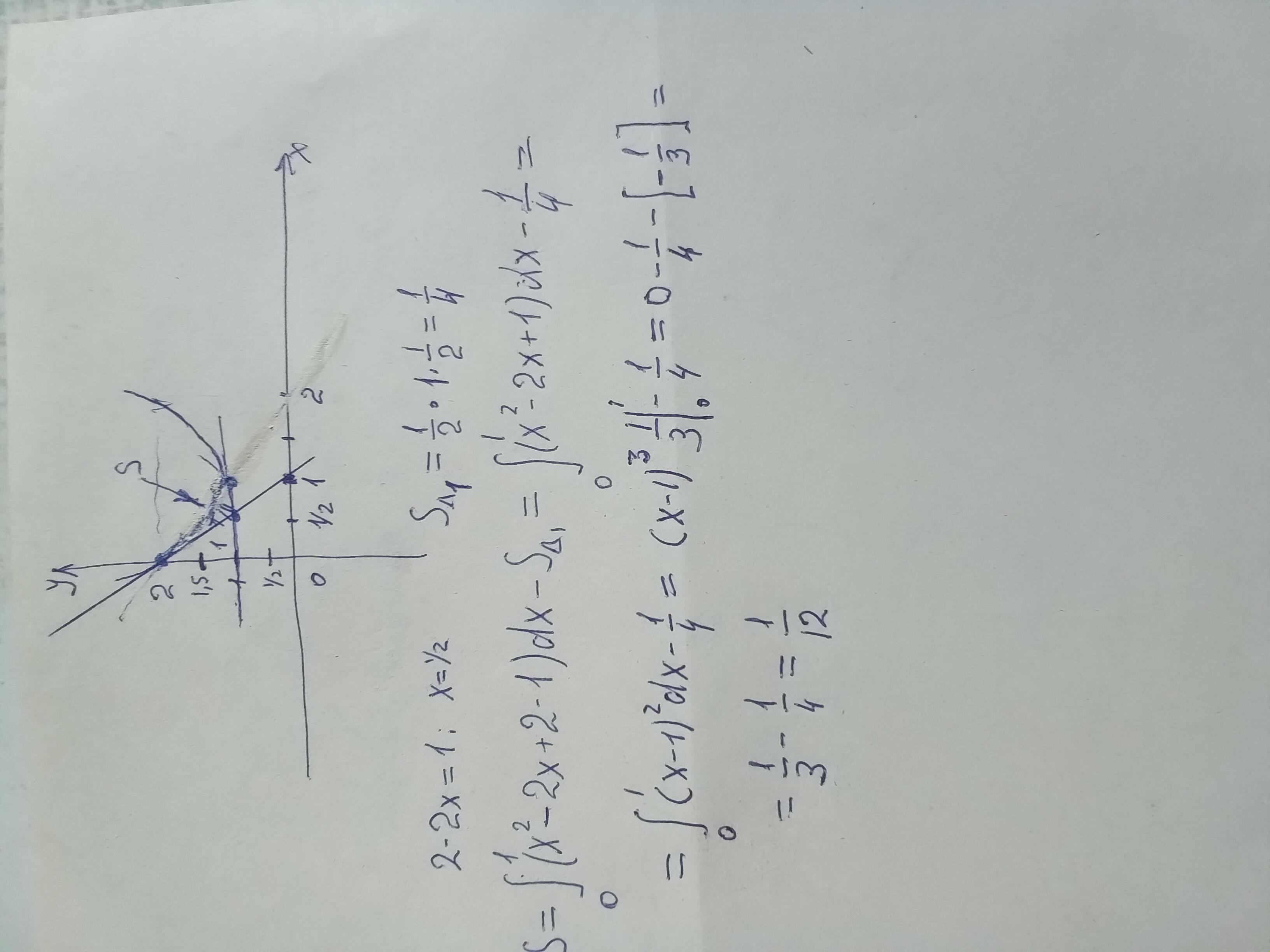
№ 2. Вычислить площадь фигуры, ограниченной прямой у = 1, параболой
у = х^2- 2х + 2 касательной, проведѐнной к этой параболе в точке еѐ пересечения с осью ординат.
Ответы
Автор ответа:
1
Ответ:
1/12
Объяснение:
х=0 у=2
уравнение касательной в точке х0 =0
у=у(0)+у'(0)(х-0)
у'=2х-2
у'(0)=-2
у=2-2х
Приложения:
Автор ответа:
2
Объяснение:
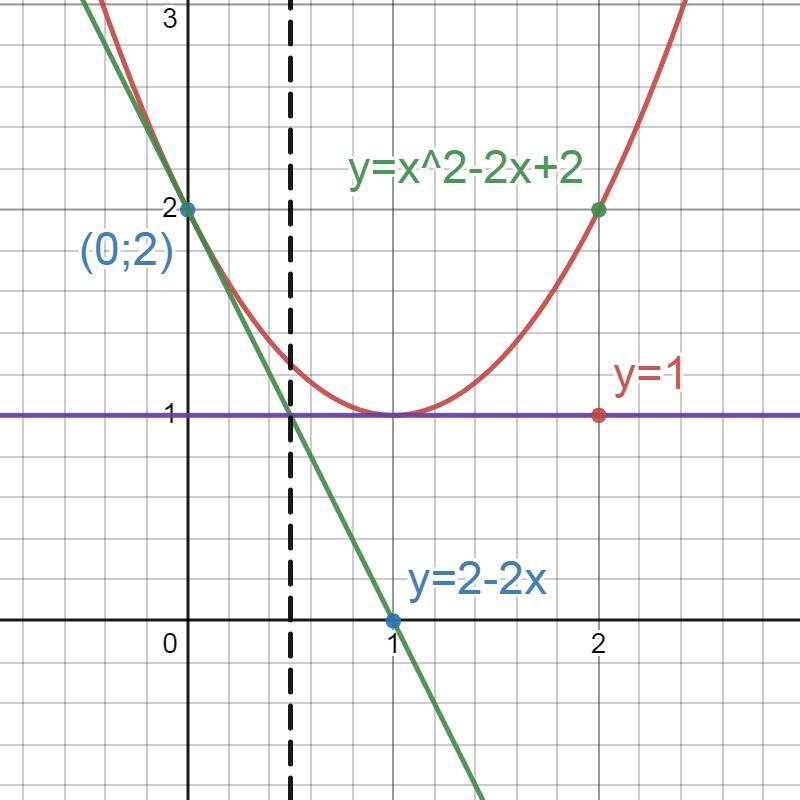
Это график функции у=х², смещённый: на 1 единицу вправо вдоль оси ОХ и поднятый вверх на 1 единицу вдоль оси ОУ (см.Рис.).
Найдём касательную к графику у=х²-2х+2 в точке х=0.
Ответ: S=0,083333 кв. ед.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: 123455678901
Предмет: Русский язык,
автор: Sergey2k
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: trrodjxcbdbsjjdf