Question

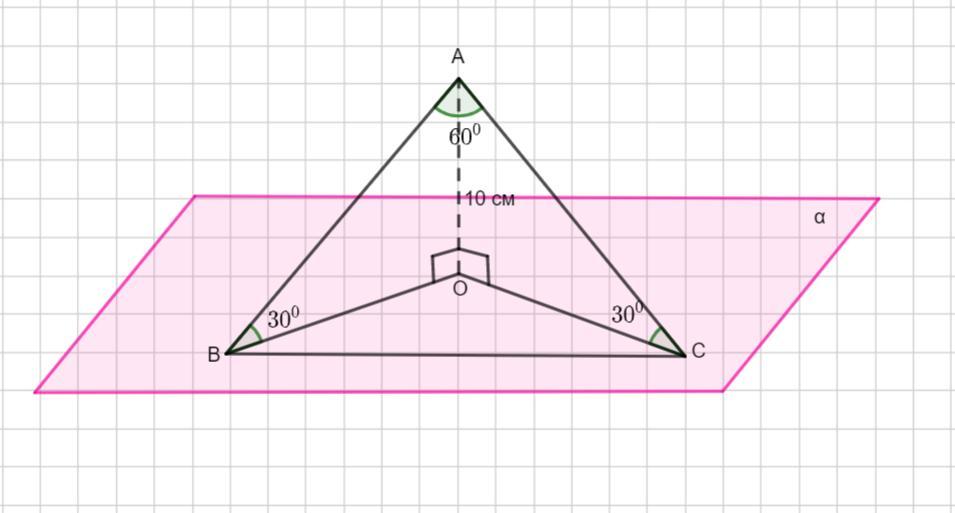
. Из точки, удаленной от плоскости на расстоянии 10 см, проведены две
наклонные, образующие с плоскостью углы в 30градусв
, а угол между ними равен
60градусов
. Найти расстояние между концами наклонных.

Answer 1

Ответ:

Расстояние между концами наклонных равно 20 см.

Пошаговое объяснение:

Из точки, удаленной от плоскости на расстояние 10 см, проведены две наклонные, образующие с плоскостью углы в 30°, а угол между ними 60°. Найти расстояние между концами наклонных.

Рассмотрим рисунок . АО- перпендикуляр к плоскости α, АО= 10 см.

АВ и АС - наклонные.

∠АВО=∠АСО= 30°, а угол между наклонными ∠ВАС = 60°. Надо найти ВС - расстояние между концами наклонной.

Рассмотрим ΔАОВ - прямоугольный, АО =10 см, ∠АВО= 30°.

По свойству катета, лежащего напротив угла в 30°.

$AB= 2\cdot AO;\\AB= 2\cdot 10=20$ см.

Аналогично, наклонная АС = 20 см.

Рассмотрим ΔАВС - равнобедренный, так как АВ=АС = 20 см.

В равнобедренном треугольнике углы при основании равны и сумма всех углов равна 180°.

Если ∠ВАС = 60°, то ∠АВС =∠АСВ =(180°-60°):2 = 60°.

Значит, ΔАВС - равносторонний, так как все углы равны 60°.

Тогда ВС= АВ =АС = 20 см.

Значит, расстояние между концами наклонных равно 20 см.

#SPJ1