Задание приложено...
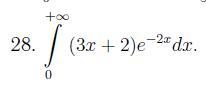
Ответы
Ответ:
Примечание:
Интегрирование по частям:
Пошаговое объяснение:
- несобственный интеграл 1 рода
Если существует предел существует конечный предел у несобственного интеграла, то данный интеграл является сходящимся.
Рассмотрим неопределенный интеграл .
а)
--------------------------------------------------------------------------------------------------------
Интегрирование по частям:
----------------------------------------------------------------------------------------------------------
б)
Для вычисления несобственного 1 рода воспользуемся двойной несобственной подстановкой:
Предел , так как
- показательная функция, то она растет быстрее чем любая линейная функция следовательно, знаменатель будет расти быстрее числителя и на бесконечности дробь стремится к нулю.
Также существует второй способ вычисления данного интеграла.
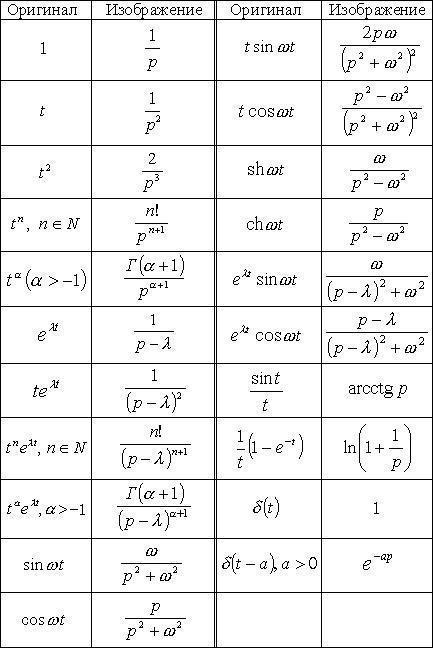
По определению преобразование Лапласа:
Где - оригинал, а
- изображение.
Для интеграла функция
является оригиналом, так как соответствует определению функции-оригинала в данном случае.
Применяя преобразование Лапласа для функции (согласно таблице) получим следующие:
Свойство линейности преобразования Лапласа:
Где и
.
Тогда так как:
То есть и для интеграла
, тогда:
.