Question

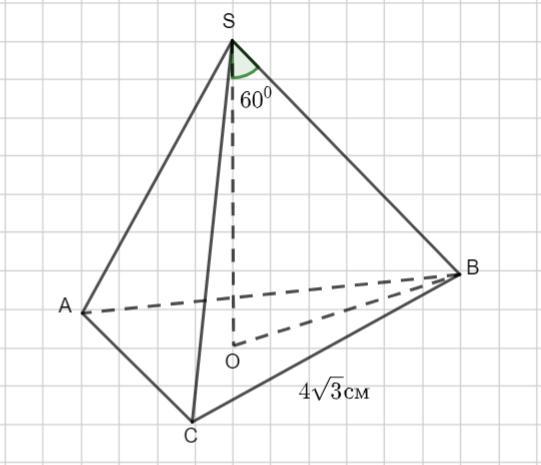
Ребро SB правильной пирамиды SABC образует угол 60° с высоты пирамиды. Сторона основания пирамиды АВ равна 4√3 см. Найдите высоту пирамиды

Answer 1

Ответ:

Высота пирамиды равна  $\dfrac{4\sqrt{3} }{3}$ см.

Пошаговое объяснение:

По условию задана правильная треугольная пирамида SABC. Ребро SВ образует с высотой угол в 60°. Сторона основания пирамиды равна 4√3 см. Надо определить высоту пирамиды.

Рассмотрим Δ SОВ - прямоугольный . Если пирамида правильная, то OB является радиусом описанной около ΔАВС окружности.

ΔАВС - правильный, тогда

$R=\dfrac{a}{\sqrt{3} } ,$

a- сторона треугольника.

$OB =R =\dfrac{4\sqrt{3} }{\sqrt{3} } =4$

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

$tg BSO= \dfrac{OB}{OS};\\\\tg60^{0} = \dfrac{4}{OS} ;\\\\\sqrt{3} =\dfrac{4}{OS};\\\\OS=\dfrac{4}{\sqrt{3} } =\dfrac{4\sqrt{3} }{3}$ см.

Значит, высота пирамиды равна  $\dfrac{4\sqrt{3} }{3}$ см.

#SPJ1