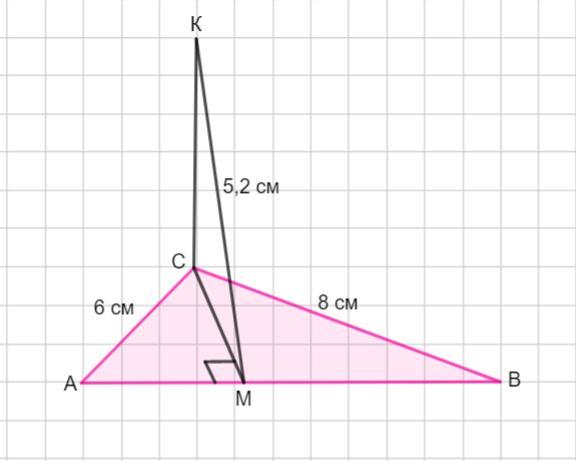
Із вершини прямого кута прямокутного трикутника проведено перпендикуляр до площини трикутника. Катети прямокутного трикутника дорівнюють 6см і 8 см. Знайдіть довжину перпендикуляра, якщо відстань від верхнього кінця перпендикуляра до гіпотенузи дорівнює 5,2 см.
Ответы
Ответ:
Длина перпендикуляра равна 2 см.
Пошаговое объяснение:
По условию задан Δ АВС - прямоугольный, ∠С =90°.
Катеты АС =6 см, ВС =8 см. Из вершины прямого угла проведен перпендикуляр СК к плоскости треугольника. Расстояние от точки К до гипотенузы КМ =5,2 см. Надо найти длину перпендикуляра СК.
Если КМ - это расстояние от точки К до гипотенузы АВ , то КМ ⊥АВ.
СК ⊥( пл. АВС) . Тогда по теореме о трех перпендикулярах проекция наклонной СМ⊥ АВ и отрезок СМ - высота ΔАВС.
Чтобы найти высоту прямоугольного треугольника, проведенную к гипотенузе, надо произведение катетов разделить на гипотенузу.
Найдем гипотенузу АВ, применяя теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
см.
Тогда высота СМ
см.
Рассмотрим Δ КСМ - прямоугольный и применим теорему Пифагора
Значит, длина перпендикуляра равна 2 см.
#SPJ1