Найди экстремумы функции б) y = (x-2)^2 e^x-3
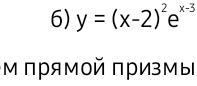
Ответы
Ответ:
;
- экстремумы функции
Пошаговое объяснение:
Найти экстремумы функции:
Областью определения данной функции является множество всех действительных чисел.
D(y) = (-∞; +∞)
Найдем производную функции. Для этого воспользуемся правилом дифференцирования производной
где u,v - дифференцируемые функции.
Найдем критические точки, решив уравнение:
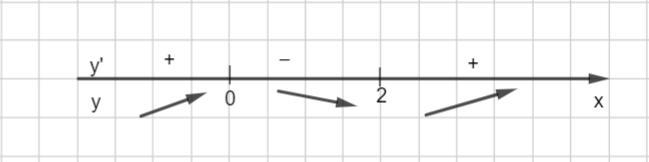
Критические точки разбивают числовую прямую на три промежутка.
Определим знак производной на каждом промежутке ( во вложении)
Если при переходе через точку производная меняет свой знак с "+" на "-", то данная точка является точкой максимума .
Если при переходе через точку производная меняет свой знак с "-" на "+", то данная точка является точкой минимума.
Тогда
Найдем экстремумы функции. Для этого найдем значение функции в точках экстремума .
#SPJ1