Предмет: Математика,
автор: shevchenkoanuta
Помогите пожалуйста решить:
Представить двойной интеграл (на прикрепленном фото) в виде повторного интеграла с внешним интегрированием по х и внешним интегрированием по у, если область D задана указанными линиями ( на прикрепленном фото).
Приложения:
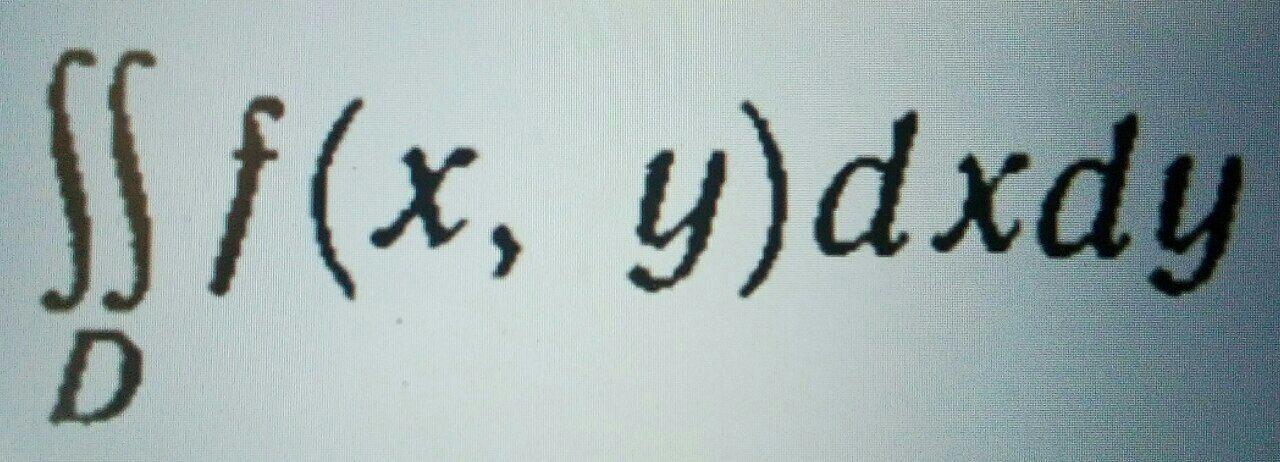
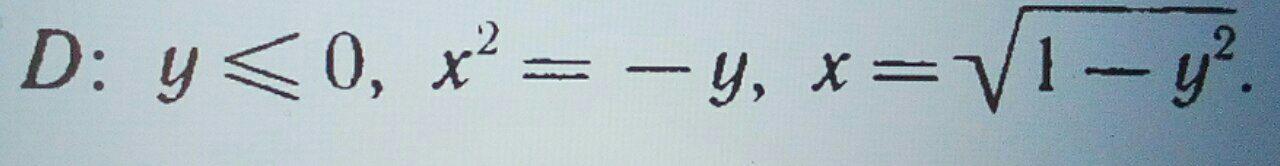
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
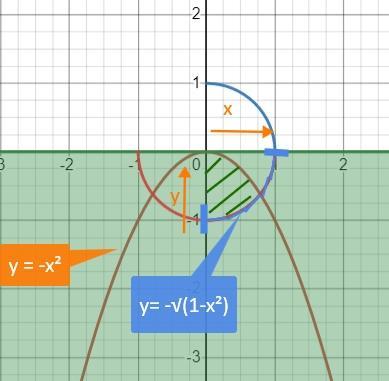
Прежде всего делаем чертеж и определяем, что х изменяется от 0 до 1, а у изменяется от до -x².
Как мы это получили?
Нам надо выразить y через x и сохранить графики, которые заданы условиями.
x² = -y ⇒ y = -x²
Второе уравнение представляет собой уравнение окружности, ее "правую" часть. Из этой правой части в нашу область интегрирования попадает только часть окружности в четвертой четверти. Эту часть окружности мы можем получить и из "нижней" части окружности, которая выражается формулой
.
Таким образом, мы получили пределы интегрирования
х от 0 до 1
у от до -x² -√(1-x²)
И тогда получим такой повторный интеграл
#SPJ1
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: Бату0323
Предмет: Английский язык,
автор: 03022006sss
Предмет: Русский язык,
автор: voynova87
Предмет: Алгебра,
автор: ddt235
Предмет: Русский язык,
автор: Аноним