Задание приложено...
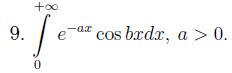
Ответы
Ответ:
Примечание:
Интегрирование по частям:
Пошаговое объяснение:
- несобственный интеграл 1 рода
Если существует предел существует конечный предел у несобственного интеграла, то данный интеграл является сходящимся.
Рассмотрим неопределенный интеграл .
----------------------------------------------------------------------------------------------------------
Интегрирование по частям:
----------------------------------------------------------------------------------------------------------
----------------------------------------------------------------------------------------------------------
Интегрирование по частям:
----------------------------------------------------------------------------------------------------------
Для вычисления несобственного 1 рода воспользуемся двойной несобственной подстановкой:
