Предмет: Математика,
автор: Reideen
Задание приложено...
Приложения:
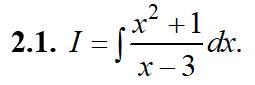
Ответы
Автор ответа:
1
Ответ:
, С ∈ ℝ
Пошаговое объяснение:
Автор ответа:
1
Ответ:
Примечание:
По таблице интегралов:
По свойствам интегралов:
Пошаговое объяснение:
--------------------------------------------------------------------------------------------------------
Замена:
--------------------------------------------------------------------------------------------------------
Похожие вопросы
Предмет: Қазақ тiлi,
автор: гульнара36
Предмет: Английский язык,
автор: Кармен51
Предмет: Қазақ тiлi,
автор: madina2005g
Предмет: Психология,
автор: Chelovek20021
Предмет: Математика,
автор: stepan6847