Предмет: Алгебра,
автор: Alexxx0013
нужно найти dx/dy и d^2y/dx^2
Приложения:
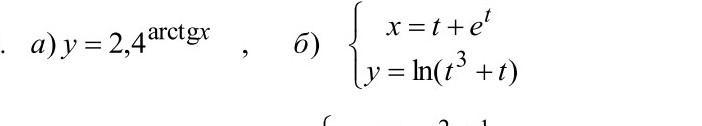
Ответы
Автор ответа:
1
Ответ:
Первую производную находим по правилу дифференцирования показательной функций .
Вторую производную находим как производную произведения функций .
Производная функции , заданной параметрически .
Вторая производная .
Alexxx0013:
огромное спасибо
если есть время, посмотрите и другую задачу пожалуйста)
вы здесь
Похожие вопросы
Предмет: Русский язык,
автор: anadon12839
Предмет: Русский язык,
автор: ксюня193
Предмет: Английский язык,
автор: Marintos7
Предмет: Русский язык,
автор: rasul5955