Question

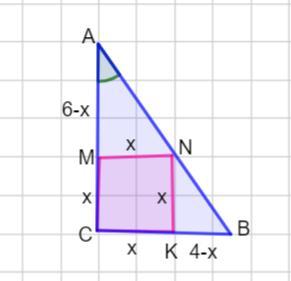
Дан Прямоугольный треугольник ABC угол C равен 90°, AC равно 6, BC равно 4,В этом прямоугольным треугольнике построен квадрат,Найдите сторону квадрата

Answer 1

Ответ:

Сторона квадрата равна 2,4 ед.

Пошаговое объяснение:

Дан прямоугольный Δ АВС , ∠С=90°, АС =6 ед., ВС = 4 ед.

В этот прямоугольный треугольник вписан квадрат CMNK.

Найти сторону квадрата.

Пусть сторона квадрата равна х ед., то есть

CM = MN = NK = СК =х ед. Тогда AM= (6-x) ед.  , KB=(4-x) ед.

Сумма острых углов прямоугольного треугольника равна 90°.

В ΔАВС - прямоугольном ∠А +∠В=90°.

ΔAMN - прямоугольный и  ∠NAM +∠ANM=90°.

ΔMAN  подобен ΔCAB по двум углам.( ∠A - общий, ∠ANM=∠ABC)

Если треугольники подобны, то составим пропорцию

$\dfrac{AM}{AC} =\dfrac{MN}{BC} ;\\\\\dfrac{6-x}{6} =\dfrac{x}{4}$

Воспользуемся основным свойством пропорции: в верной пропорции произведение крайних членов пропорции равно произведению средних членов.

$4\cdot(6-x)=6x;\\24-4x=6x;\\24=6x+4x;\\10x=24;\\x=24:10;\\x=2,4$

Значит, сторона квадрата равна 2,4 ед.

#SPJ1