Предмет: Математика,
автор: ustrica1111
найдите производную заданной функций
учитель просит упростить,я уже это сделала,дальше не знаю как решать.заранее спасибо
Приложения:
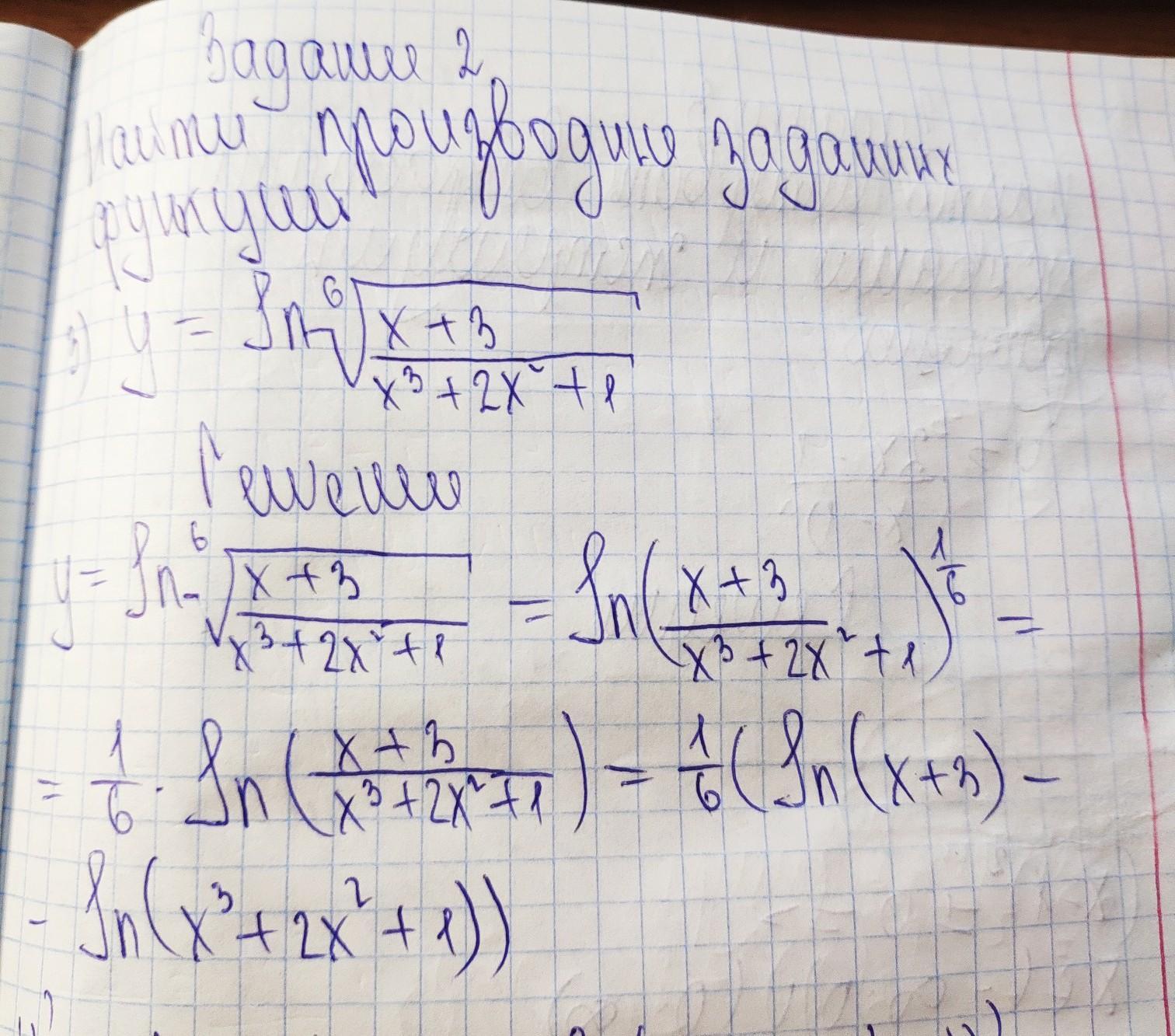
ВикаБач:
Может она хочет, чтобы это был логарифм дроби(частного)?
я могу скинуть пример ее решения
только не знаю куда можно его отправить
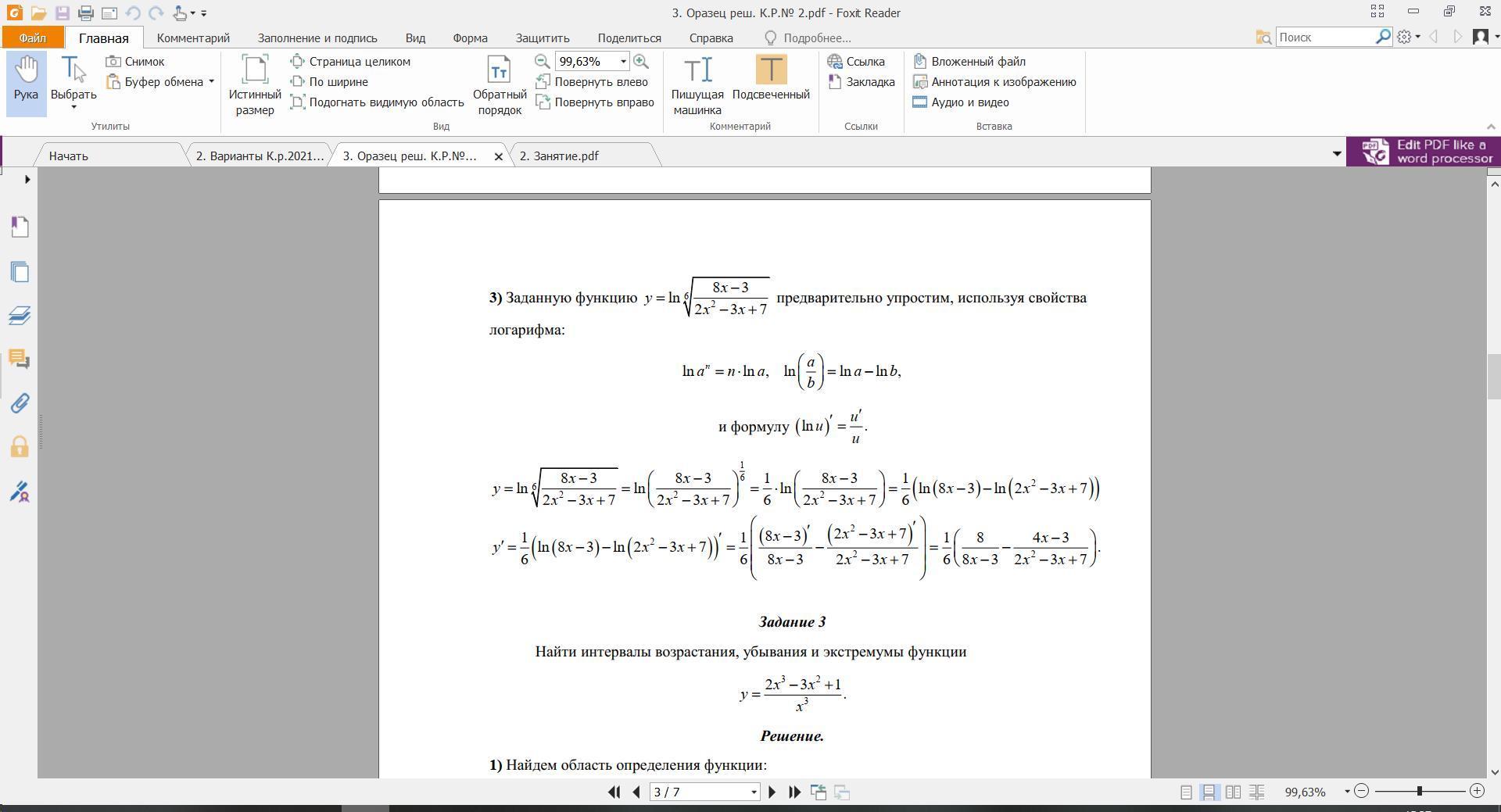
я добавила пример решения в вопрос
Ну да, она этого и хочет... Просто lnA-lnB=ln(A/B) этим и играются.
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
Требуется найти производную от функции
Преобразуем вид функции:
Вычислим производную от функции:
#SPJ1
Похожие вопросы
Предмет: Русский язык,
автор: amulka777
Предмет: Русский язык,
автор: Коляный228
Предмет: Русский язык,
автор: кисуня50
Предмет: Математика,
автор: lezepekova87
Предмет: Физика,
автор: Аноним