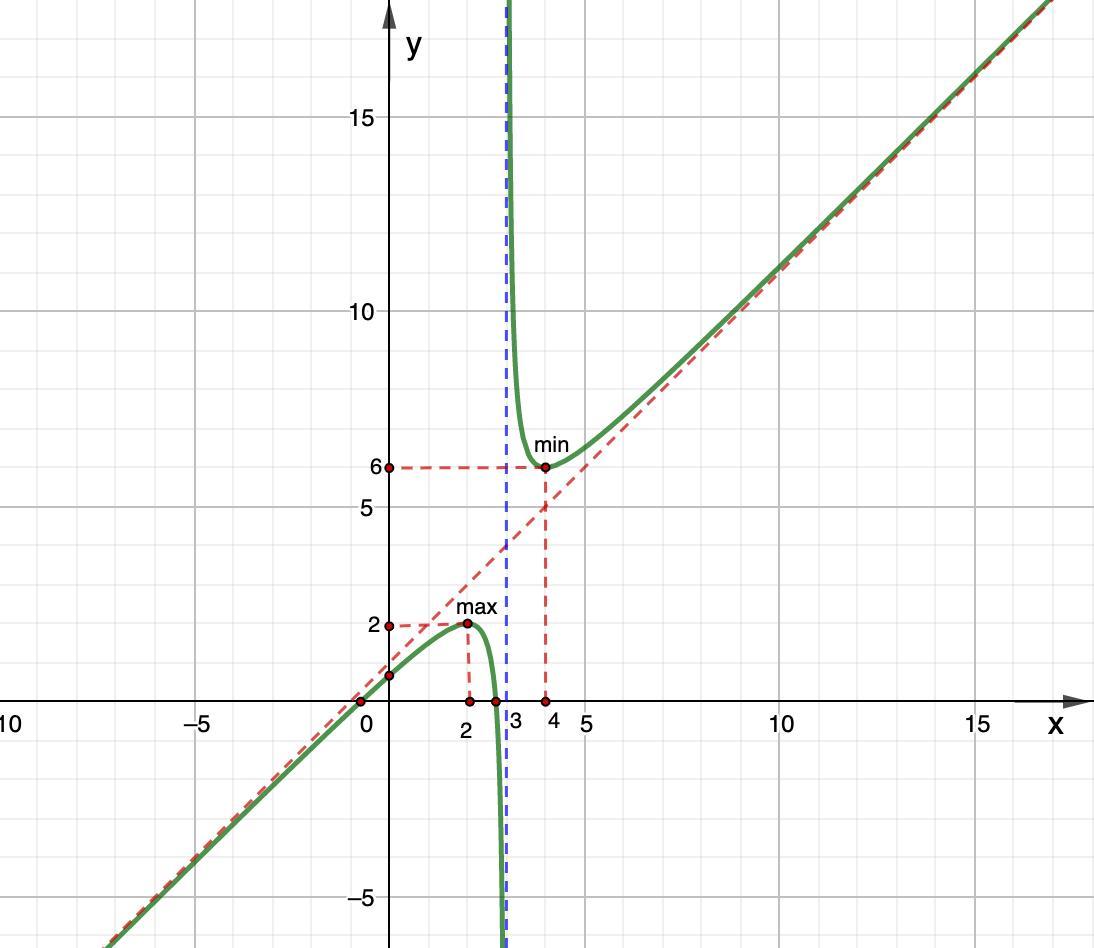
Исследование и построение графика функции y(x)=x^2-2x-2/x-3
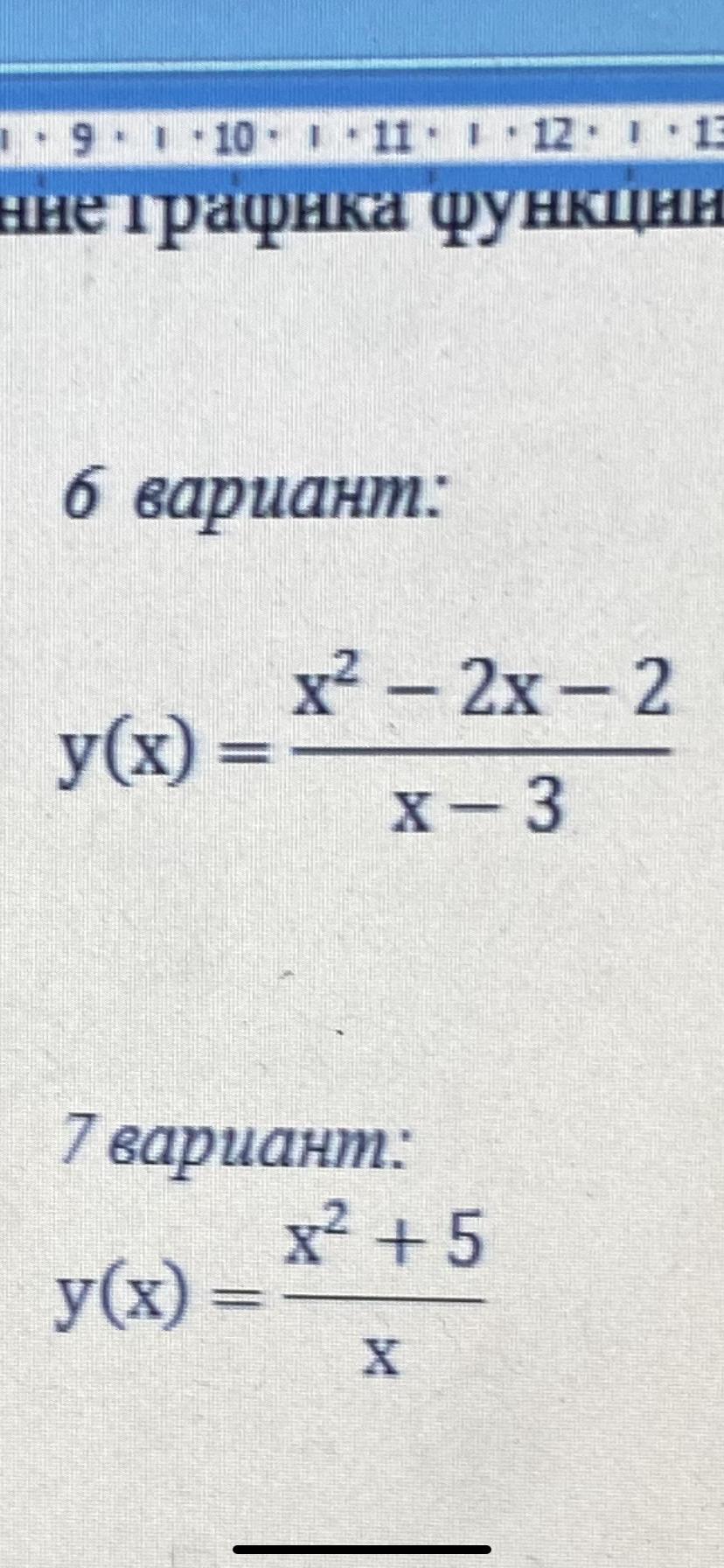
Ответы
Ответ:
1. ОДЗ: х ∈ (-∞; 3)∪(3; +∞).
2. Функция не является четной или нечетной, то есть общего вида.
3. х = 0 ⇒ у = 0,7;
у = 0 ⇒ x₁ = 2,7; x₂ = - 0,7.
4. x = 3 - вертикальная асимптота.
y = x + 1 - наклонная асимптота.
5. Функция возрастает на промежутках: (-∞; 2], [4; +∞).
Функция убывает на промежутках: [2; 3), (3; 4].
х max = 2; x min = 4.
6. Функция выпукла на промежутке (-∞; 3).
Функция вогнута на промежутке (3; +∞).
Объяснение:
Исследование и построение графика функции
1. ОДЗ: х ≠ 3
или х ∈ (-∞; 3)∪(3; +∞)
2. Четность, нечетность.
Если f(-x) = f(x), то функция четная, если f(-x) = -f(x) - нечетная.
y(-x) ≠ y(x) ≠ -y(x) ⇒ функция не является четной или нечетной, то есть общего вида.
3. Пересечение с осями.
1) х = 0 ⇒ у = 2/3 ≈ 0,7
2) у = 0 ⇒ х² - 2х -2 = 0
х² - 2х + 1 - 3 = 0
(х - 1)² - (√3)² = 0
(x - 1 - √3)(x - 1 + √3) = 0
x₁ = 1 + √3 ≈ 2,7
x₂ = 1 - √3 ≈ - 0,7
4. Асимптоты.
1)
⇒ x = 3 - вертикальная асимптота.
2) Наклонная асимптота: y = kx + b
⇒ y = x + 1 - наклонная асимптота.
5. Возрастание, убывание, экстремумы.
Найдем производную, приравняем к нулю, найдем корни.
Отметим их на числовой оси и определим знак производной на промежутках.
- Если "+", то функция возрастает, если "-" - убывает.
y' = 0
По теореме Виета:
х₁ = 2; х₂ = 4
у(2) = 2; у(4) = 6
Не забываем про х ≠ 3
Функция возрастает на промежутках: (-∞; 2], [4; +∞).
Функция убывает на промежутках: [2; 3), (3; 4].
- Если производная меняет знак с плюса на минус, то в данной точке наблюдается максимум, если с минуса на плюс, то в данной точке - минимум.
⇒ х max = 2; x min = 4.
6. Выпуклость, вогнутость.
Найдем производную второго порядка, приравняем к нулю и найдем корни.
Отметим их на числовой оси.
- Если производная второго порядка положительна, функция вогнута, если отрицательна - выпукла.
Имеем одну точку х ≠ 3
Функция выпукла на промежутке (-∞; 3).
Функция вогнута на промежутке (3; +∞).
Строим график.
#SPJ1