Предмет: Геометрия,
автор: Xefar
Решите пожалуйста с рисунком, даю 40 баллов!!!
обчислити бокову поверхню правильної трикутної піраміди висота якої дорівнює h а двогранний кут при основі дорівнює альфа.
вычислить боковую поверхность правильной треугольной пирамиды высота которой равна h а двухгранный угол при основании равен альфа
Ответы
Автор ответа:
2
Ответ:
Площадь боковой поверхности равна ед².
Объяснение:
Вычислить боковую поверхность правильной треугольной пирамиды, высота которой равна h, а двугранный угол при основании равен α.
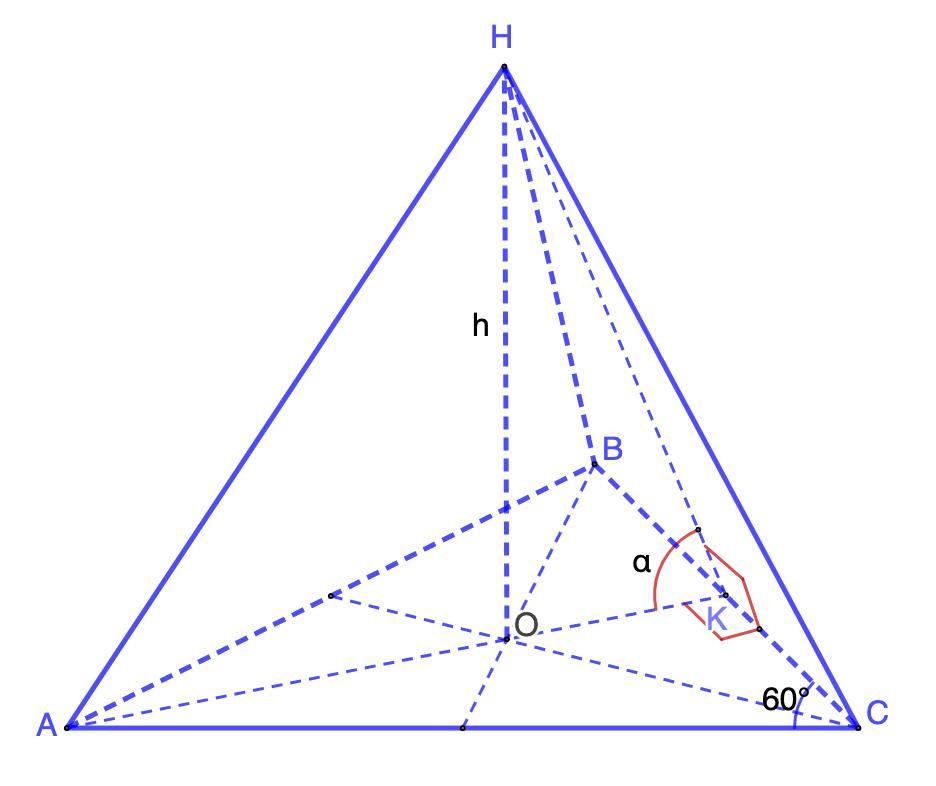
Дано: НАВС - правильная пирамида;
НО = h - высота;
НКА = α - линейный угол двугранного угла НВСА;
Найти: S бок.
Решение:
- Двугранный угол — это часть пространства, заключённая между двумя полуплоскостями, имеющими одну общую границу.
- Градусной мерой двугранного угла называется градусная мера его линейного угла.
- Площадь боковой поверхности пирамиды равна произведению полупериметра основания на апофему:
- S = pd, где р - полупериметр; d - апофема.
1. Найдем апофему НК.
Рассмотрим ΔОНК - прямоугольный.
- Синус угла - отношение противолежащего катета к гипотенузе.
2. Теперь нам надо найти периметр основания.
Рассмотрим ΔОНК - прямоугольный.
- Тангенс - отношение противолежащего катета к прилежащему.
- В основании правильной пирамиды лежит правильный треугольник.
- Все высоты равностороннего треугольника являются медианами.
- Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2 : 1, начиная от вершины.
⇒
Рассмотрим ΔАКС - прямоугольный.
- Градусная мера углов равностороннего треугольника равна 60°.
⇒
Найдем полупериметр:
3. Найдем площадь боковой поверхности:
Площадь боковой поверхности равна ед².
#SPJ1
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: lady54
Предмет: Русский язык,
автор: марила1
Предмет: Русский язык,
автор: Даша21234
Предмет: Математика,
автор: Elisey13
Предмет: Физика,
автор: pochtalyon7