Предмет: Математика,
автор: yurabogomolov2004
Розкладання в ряд Тейлора –Маклорена фунції y= sin x.
2 задание на картинке
Приложения:
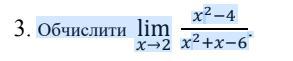
Ответы
Автор ответа:
1
Ответ:
1)
2)
Пошаговое объяснение:
Розкладання в ряд Тейлора –Маклорена фунції y= sin x - это ростейшее табличное разложение синуса в степенной ряд/
3) Поскольку и числитель и знаменатель обращаются в 0 при х = 2, число х=2 является одним из корней обоих уравнений.
Разложим числитель и знаменатель на множители.
(x² - 4 ) = (x +2)(x - 2)
x² +x - 6 = (x-2)(x+3)
И тогда мы легко считаем предел
#SPJ1
solka0000:
будь ласка ,я закинула тепер завдання допоможіть ,будь ласка
даю максимум балів
з математики
дискретную математику я решила Вам
Похожие вопросы
Предмет: Английский язык,
автор: Jq4731
Предмет: Русский язык,
автор: missmixailo
Предмет: Українська література,
автор: 265224
Предмет: Українська мова,
автор: fistel14848
Предмет: Право,
автор: 1Sharik1