Question

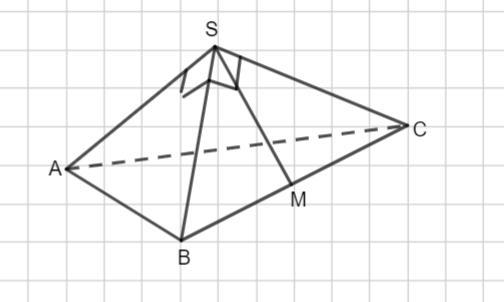
Плоский угол при вершине правильной треугольной пирамиды равен 90°. Найдите площадь боковой поверхности пирамиды, если радиус окружности, описанной около ее боковой грани, равен 4√3​

Answer 1

Ответ:

Площадь боковой поверхности равна 144 кв. ед.

Объяснение:

По условию задана SABC - пирамида. Плоский угол при вершине равен 90°, то есть ∠ASB=∠ASC=∠BSC=90°.

Надо найти площадь боковой поверхности, если радиус окружности описанной около боковой грани равен 4√3 ед.

Если плоские углы при вершине прямые, то каждая боковая грань есть прямоугольный, равнобедренный  треугольник.

Радиус окружности, описанной около прямоугольного треугольника равен половине гипотенузы. Тогда

$AB=BC =AC =2R=2\cdot 4\sqrt{3} =8\sqrt{3}$ ед.

Площадь боковой поверхности равна утроенной площади боковой грани. Проведем в грани BCS высоту, медиану и биссектрису SМ.

Медиана прямоугольного треугольника, проведенная к гипотенузе равна ее половине.

$SM= \dfrac{1}{2} BC;\\\\SM= \dfrac{1}{2} \cdot 8\sqrt{3}=4\sqrt{3}$

Если SM и высота, то найдем площадь треугольника как полупроизведение стороны на высоту, проведенную к данной стороне.

$S{_{BCS}}=\dfrac{1}{2} \cdot BC\cdot SM;\\\\S{_{BCS}}=\dfrac{1}{2} \cdot 8\sqrt{3} \cdot 4\sqrt{3} =4\cdot4\cdot3=48$  кв. ед.

Если площадь одной боковой грани равна 48 кв.ед., то площадь боковой поверхности в 3 раза больше

$S= 48\cdot3=144$ кв. ед.

#SPJ1