Предмет: Математика,
автор: novikovadashaa
Срочно! решить задачу Коши!!
Приложения:
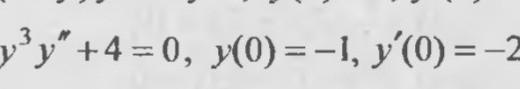
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
y³y''+4=0 - это дифференциальное уравнение 2-го порядка, допускающее понижение порядка благодаря тому, что в уравнении в явном виде нет аргумента x. В этом случае теория рекомендует замену y'=p(y), при этом y''=p'p (не забывайте, что y является функцией от x и производную от y' берем по x, а p является функцией от y, поэтому Мы воспользовались формулой производная слолжной функции. Получаем
Подставив начальные условия, находим C:
Снова подставляем начальные условия, чтобы определиться со знаком:
поэтому выбираем плюс,
Еще раз подставляем начальные условия:
Чтобы определиться со знаком, опять обращаемся к начальным условиям:
поэтому выбираем минус. Окончательно
novikovadashaa:
Спасибо большое!!
Похожие вопросы
Предмет: Русский язык,
автор: dfdfdfdfdfdfdfdfdf
Предмет: Русский язык,
автор: ксюша1335
Предмет: Русский язык,
автор: Аноним
Предмет: География,
автор: hjdtii
Предмет: Беларуская мова,
автор: Аноним