Question

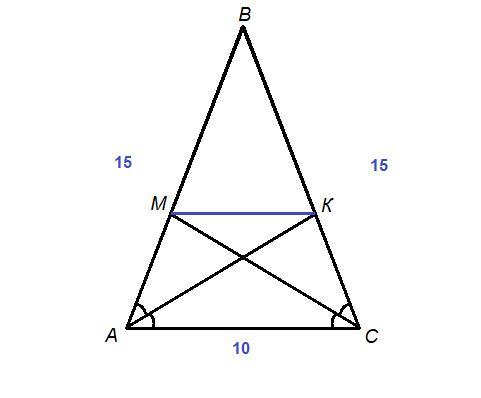
. Боковая сторона равнобедренного треугольника равна
15 см, а основание – 10 см. К боковым сторонам
треугольника проведены биссектрисы. Найдите длину
отрезка, концами которого являются основания
биссектрис.

Answer 1

Ответ:

6 см

Объяснение:

ΔАВС равнобедренный, АК и СМ - биссектрисы.

Свойство биссектрисы треугольника:

• биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам.

$\dfrac{BM}{MA}=\dfrac{BC}{AC}=\dfrac{15}{10}=\dfrac{3}{2}$     ⇒     $\dfrac{BM}{AB}=\dfrac{3}{5}$

$\dfrac{BK}{KC}=\dfrac{AB}{AC}=\dfrac{15}{10}=\dfrac{3}{2}$     ⇒     $\dfrac{BK}{BC}=\dfrac{3}{5}$

Так как угол В общий для треугольников МВК и АВС, то треугольники подобны по двум пропорциональным сторонам и углу между ними.

$\dfrac{MK}{AC}=\dfrac{3}{5}$

$MK=\dfrac{3\cdot AC}{5}=\dfrac{3\cdot 10}{5}=3\cdot 2=6$  см