Помогите срочно!!!!!!!"
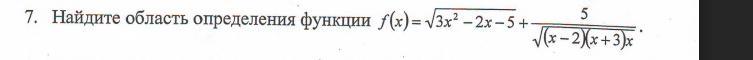
Ответы
Ответ:
подкоренное выражение должно быть больше либо равное 0. найдем нулевые точки первого корня
нарисуем прямую и укажем наши точки. узнаем знаки на интервале, чтобы выбрать те, что больше либо равны 0.
нам подходит от минус бесконечности до -1 включительно и от 5/3 включительно до бесконечности.
перейдем ко второму члену многочлена
здесь корень находится в знаменателе, т.к. это знак корня, то подходят только значения равные или больше 0, но т.к. в знаменателе, то равные 0 не подходят.
сразу видно что х не может быть равен 2, -3, 0.
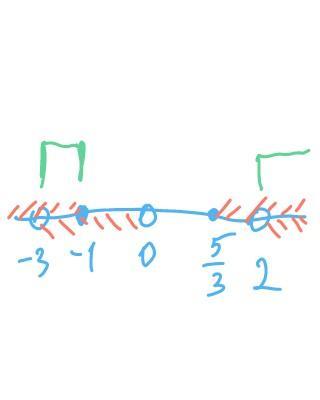
рисуем прямую, отмечаем точки и узнаем знаки.
нам подходит от -3 невключительно до 0 невключительно, от 2 невключительно до бесконечности.
объединяем оба результата
область определения функции от -3 невключительно до -1 включительно и от 2 невключительно до бесконечности.
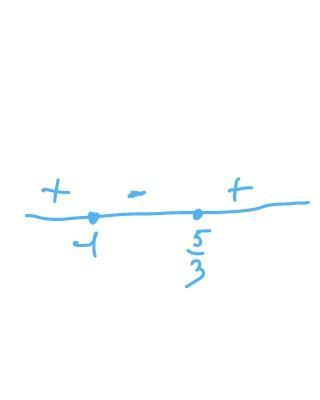

Объяснение:
ОДЗ:
(x+1)*(3x-5)≥0
-∞__+__-1__-__5/3__+__+∞ ⇒
x∈(-∞;-1]U[5/3;+∞).
(x-2)*(x+3)*x>0
-∞__-__-3__+__0__-__2__+__+∞ ⇒
x∈(-3;0)U(2;+∞).
Ответ: x∈(-3;-1]U(2;+∞).