Предмет: Геометрия,
автор: ktojeyatakoy
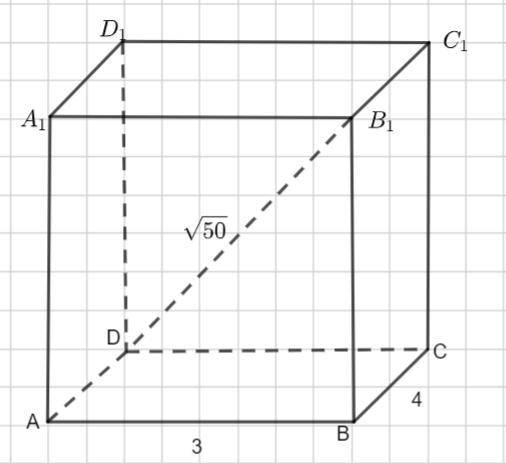
В прямоугольном параллелепипеде abcda1b1c1d1, ab=3, bc=4, b1d=√50
скольки будет ровняться длина стороны bb1?
BMW52:
ВВ1=√(50-25) =√25=5
Ответы
Автор ответа:
0
Ответ:
Длина отрезка равна 5 ед.
Объяснение:
Пусть дан прямоугольный параллелепипед .
АВ =3 ед., ВС =4 ед. ед.
диагональ прямоугольного параллелепипеда. Надо найти длину
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов его измерений, то есть
a- длина
b- ширина
c- высота
Отрезок является высотой прямоугольного параллелепипеда.
Тогда
Значит, длина отрезка равна 5 ед.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Angel2021
Предмет: Другие предметы,
автор: ВИТУСЬКАУЛЫБУСЬКА
Предмет: Русский язык,
автор: ilhamabasov
Предмет: Математика,
автор: amos1920