Предмет: Математика,
автор: soni4ka0590
f(x) = x ^ 3 - 3x ^ 2 - 19x + 7 знайти проміжок на якому функція спадає
Ответы
Автор ответа:
0
Ответ:
Функция убывает на
Пошаговое объяснение:
Найти промежутки убывания функции
Областью определения данной функции является множество всех действительных чисел
D(f) = ( - ∞ ; + ∞)
Найдем производную данной функции
Найдем критические точки, решив уравнение :
Полученные критические точки разбивают числовую прямую на три промежутка. Определим знак производной на каждом промежутке ( во вложении)
Если на некотором промежутке, то функция убывает на данном промежутке.
Функция непрерывна в точках и
Тогда функция убывает на
#SPJ1
Приложения:
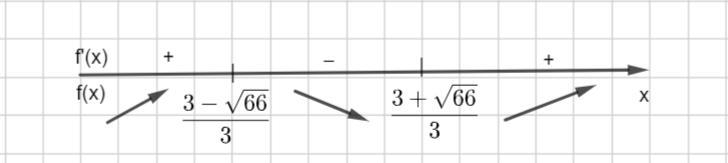
Похожие вопросы
Предмет: Русский язык,
автор: Konowalowjeny
Предмет: Қазақ тiлi,
автор: Slize
Предмет: Русский язык,
автор: SVETAKIDAROVA
Предмет: Математика,
автор: makser79No
Предмет: Математика,
автор: dilimmuratov