Предмет: Алгебра,
автор: kentofarchik
Решите пожалуйста данное задание
Приложения:
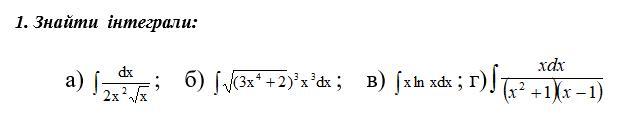
Ответы
Автор ответа:
0
Объяснение:
Применяем метод неопределённых коэффициентов:
Приравниваем коэффициенты при одинаковых степенях:
sangers1959:
Я решаю дальше.
здравствуйте помогите пожалуйста решить задачу
можете?
Всё.
Да. помогу.
Площадь фигуры?
да , там написано, и еще один дифференциально уравнения подробно нужно решить
как там с В и Г
В и Г я решил. Это с) и d).
Диф. уравнение я не нашёл.
Похожие вопросы
Предмет: Русский язык,
автор: akadmurod80
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: Муза111111
Предмет: Химия,
автор: Oven05