Предмет: Математика,
автор: Tgggghjgxsdthjkkfdhj
СРОЧНО!!!
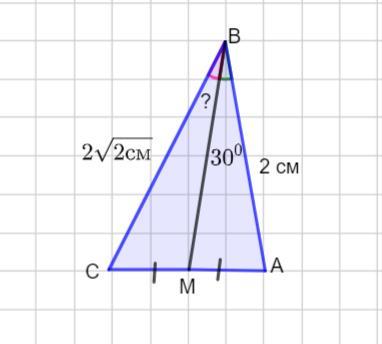
В треугольнике ВМ-медиана.угол ABM=30 градусов,АВ=2см,ВС=2корней из двух.
Найдите угол MBC
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
В треугольнике Δ АВС проведена медиана ВМ. ∠АВМ =30°,
АВ =2 см, ВС = 2√2 см. Найти ∠МВС.
Медиана треугольника делит треугольник на два равновеликих треугольника.
Тогда
Площадь треугольника найдем как полупроизведение двух сторон на синус угла между ними.
Пусть ∠МВС=α.
Так как площади треугольников равны, то получим равенство
Тогда
#SPJ1
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: Муза111111
Предмет: Русский язык,
автор: avdeevarcadiy
Предмет: Математика,
автор: dasha20074681
Предмет: Алгебра,
автор: Аноним