Предмет: Математика,
автор: novikovadashaa
Срочно! Решить дифф.уравнение первого порядка.
Приложения:
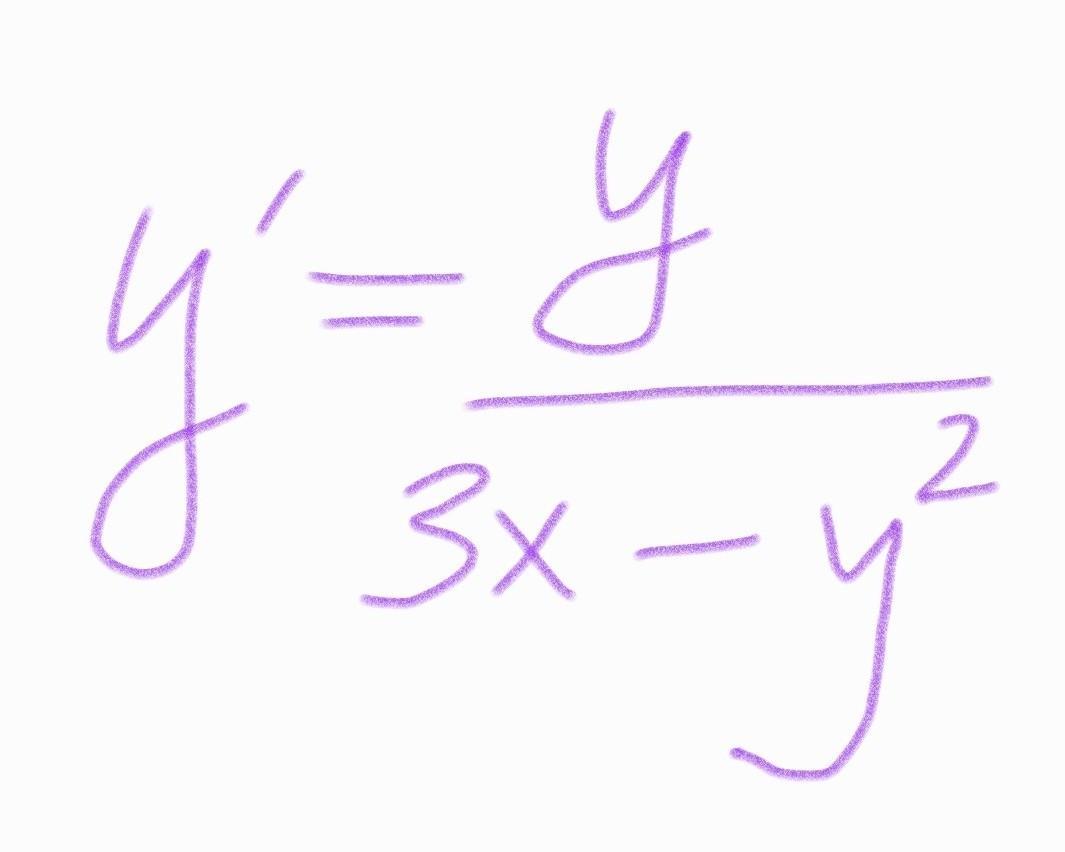
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
В принципе это уравнение можно решить как линейное уравнение относительно x как функции от y. Но, поскольку автор не указывает конкретный способ решения задачи, выберем более изысканный.
Сначала выделяем решение y=0 (левая и правая части при y=0 равны нулю). Далее преобразуем:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: алинаееее
Предмет: Английский язык,
автор: ket69
Предмет: Английский язык,
автор: 2003Александрушка
Предмет: Математика,
автор: emilbratan
Предмет: Физика,
автор: lizalove961