Question

Задание приложено...

Answer 1

Ответ:

4)

$\boxed{\boldsymbol{ \displaystyle \iint\limits_{D} {f(x,y)} \, dxdy= \int\limits^{2}_{0} {} \, dy \int\limits^{\sqrt{4 - y}}_{-\sqrt{4 - y}} {f(x,y)} \, dx + \int\limits^{4}_{2} {} \, dy \int\limits^{\sqrt{ y}}_{-\sqrt{y}} {f(x,y)} \, dx}}$

$\boxed{\boldsymbol{\displaystyle \iint\limits_{D} {f(x,y)} \, dxdy = \int\limits^{\sqrt{2} }_{-\sqrt{2} } {} \, dx \int\limits^{4 - x^{2} }_{x^{2} } {f(x,y)} \, dy}}$

5)

$\boxed{\boldsymbol{ \displaystyle \iint\limits_{D} {f(x,y)} \, dxdy = \int\limits^{2}_{0} {} \, dy \int\limits^{\sqrt{4 - y}}_{-\sqrt{4 - y}} {f(x,y)} \, dx + \int\limits^{4}_{2} {} \, dy \int\limits^{\sqrt{ y}}_{-\sqrt{y}} {f(x,y)} \, dx}}$

$\boxed{ \boldsymbol{ \displaystyle \iint\limits_{D} {f(x,y)} \, dxdy = \int\limits^{1 }_{0 } {} \, dx \int\limits^{1}_{-\sqrt{2x - x^{2} } } {f(x,y)} \, dy}}$

Примечание:

Если внутренний интеграл по y, то для расстановки пределов интегрирования в интеграле по y (функции) необходимо "проткнуть графики" по направлению с осью OY. И тот график, который "протыкается" первым пишем в нижний предел интегрирования.

Аналогично расставляю пределы интегрирования во внешнем интеграле мы должны с крайней слева точки пересечения графиков функций мысленно "заливать краской фигуру" по направлению вдоль оси OX. И соответственно в первую прямую, которую мы "встретим" вдоль оси OX ставим в нижний предел интегрирования по dx.

Если внутренний интеграл по x, то для расстановки пределов интегрирования в интеграле по x (функции) необходимо "проткнуть графики" по направлению с осью OX. И тот график, который "протыкается" первым пишем в нижний предел интегрирования.

Аналогично расставляю пределы интегрирования во внешнем интеграле мы должны с крайней слева точки пересечения графиков функций мысленно "заливать краской фигуру" по направлению вдоль оси OY. И соответственно в первую прямую, которую мы "встретим" вдоль оси OY ставим в нижний предел интегрирования по dy.

Объяснение:

4)

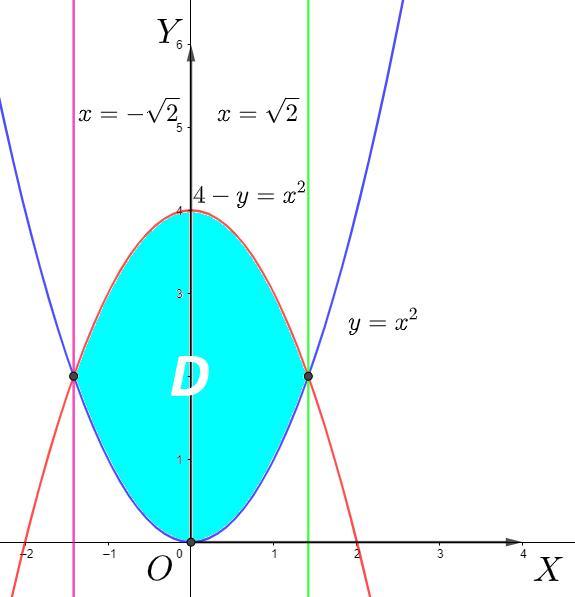
Область $D:$

$y = x^{2} \Longleftrightarrow x = \pm\sqrt{y}$

$4 - y = x^{2} \Longleftrightarrow y = 4 - x^{2} \Longleftrightarrow x = \pm\sqrt{4 - y}$

Найдем точку пересечения кривой $y = 4 - x^{2}$ и кривой $y = x^{2} :$

$4 - x^{2} = x^{2}$

$2x^{2} = 4|:2$

$x^{2} = 2 \Longrightarrow x_{1,2} = \pm \sqrt{2}$

$y = (\pm\sqrt{2})^{2} =2$

Точка $(-\sqrt{2};2)$ и $(\sqrt{2};2)$ есть точки пересечения кривой $y = 4 - x^{2}$ и кривой $y = x^{2}$.

При рассмотрении внутреннего интеграла по x, область $D$ необходимо разбить на две области $D_{1}$ и $D_{2}$. Прямая $y = 2$ разбивает  область на две области. Поэтому следует разбить интеграл на 2 области и отдельно вычислять по каждой из областей.

Внутренний интеграл по y:

$\displaystyle \iint\limits_{D} {f(x,y)} \, dxdy = \int\limits^{\sqrt{2} }_{-\sqrt{2} } {} \, dx \int\limits^{4 - x^{2} }_{x^{2} } {f(x,y)} \, dy$

Внутренний интеграл по x:

$\displaystyle \iint\limits_{D} {f(x,y)} \, dxdy =\displaystyle \iint\limits_{D_{1}} {f(x,y)} \, dxdy + \displaystyle \iint\limits_{D_{2}} {f(x,y)} \, dxdy =$

$\displaystyle = \int\limits^{2}_{0} {} \, dy \int\limits^{\sqrt{4 - y}}_{-\sqrt{4 - y}} {f(x,y)} \, dx + \int\limits^{4}_{2} {} \, dy \int\limits^{\sqrt{ y}}_{-\sqrt{y}} {f(x,y)} \, dx$

5)

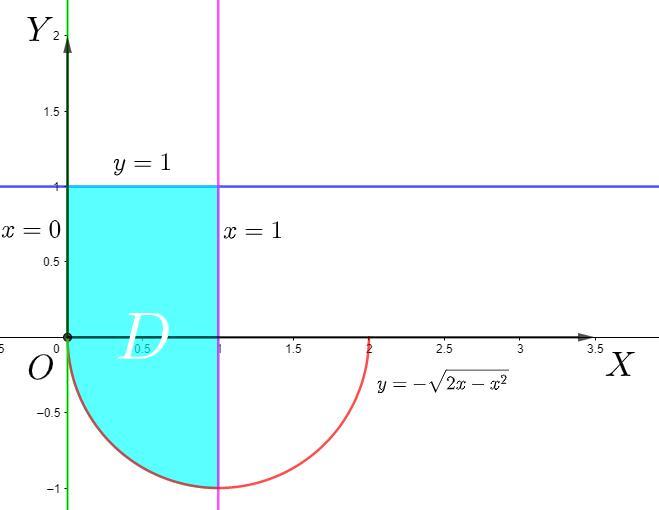
Область $D:$

$y = -\sqrt{2x - x^{2} }$

$x = 0$

$x =1$

$y = 1$

Найдем функция обратную к $y = -\sqrt{2x - x^{2} }:$

Так как $y \leq 0$, то $(-y) \geq 0$, следовательно можем возвести в квадрат обе части уравнения

$(-y)^{2} = \bigg (\sqrt{2x - x^{2} } \bigg)^{2}$

$y^{2} = 2x - x^{2}$

$y^{2} + x^{2} - 2x = 0| + 1$

$y^{2} + x^{2} - 2x + 1 = 1$

$y^{2} + (x - 1)^{2} = 1$

$(x - 1)^{2} = 1 - y^{2}$

$|x - 1| = \sqrt{1 - y^{2}}$ ( так как изначально $y = -\sqrt{2x - x^{2} }$, то раскрываем модуль с отрицательным знаком).

$-x + 1 = \sqrt{1 - y^{2}}$

$x = 1 - \sqrt{1 - y^{2}}$ - функция обратная к $y = -\sqrt{2x - x^{2} }$ при $y \in [-1;0]$.

При рассмотрении внутреннего интеграла по y, область $D$ необходимо разбить на две области $D_{1}$ и $D_{2}$. Прямая $x = 0$ разбивает  область на две области. Поэтому следует разбить интеграл на 2 области и отдельно вычислять по каждой из областей.

Внутренний интеграл по y:

$\displaystyle \iint\limits_{D} {f(x,y)} \, dxdy = \int\limits^{1 }_{0 } {} \, dx \int\limits^{1}_{-\sqrt{2x - x^{2} } } {f(x,y)} \, dy$

Внутренний интеграл по x:

$\displaystyle \iint\limits_{D} {f(x,y)} \, dxdy =\displaystyle \iint\limits_{D_{1}} {f(x,y)} \, dxdy + \displaystyle \iint\limits_{D_{2}} {f(x,y)} \, dxdy =$

$\displaystyle = \int\limits^{0}_{-1} {} \, dy \int\limits^{1}_{1- \sqrt{1 - y^{2}} } {f(x,y)} \, dx + \int\limits^{1}_{0} {} \, dy \int\limits^{1}_{0} {f(x,y)} \, dx$