Предмет: Математика,
автор: Olga19997
Обчислити похідну функції:
Фото нижче
Приложения:
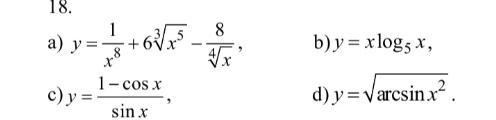
Ответы
Автор ответа:
1
Ответ:
a)
б)
c)
d)
Пошаговое объяснение:
Вычислить производную.
a)
Формула производной степенной функции:
Преобразуем данную функцию:
Найдем производную:
b)
Формулы:
Найдем производную:
c)
Формулы:
Найдем производную:
d)
Формулы производной сложной функции:
Найдем производную:
#SPJ1
Похожие вопросы
Предмет: Другие предметы,
автор: Daha265
Предмет: Английский язык,
автор: grecanka88
Предмет: Русский язык,
автор: Екатерина10011
Предмет: Математика,
автор: nataskor999
Предмет: Русский язык,
автор: tonyaZaterka