Question

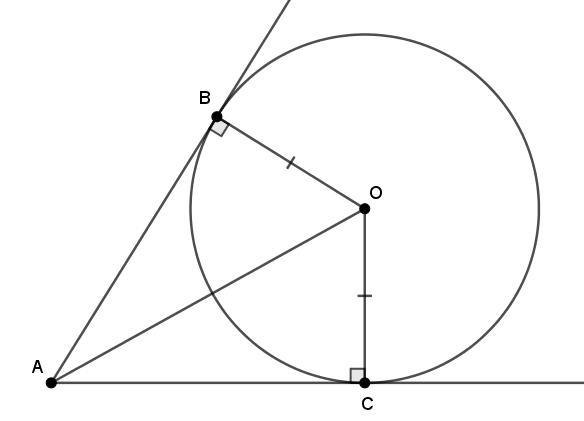
Через точку A проведено дві прямі, одна з яких дотикається до кола з центром O в точці B, а друга — в точці C. Доведіть, що промінь AO — бісектриса кута BAC.

Answer 1

Проведём радиусы в точки касания. В треугольниках AOB и AOC — BO=OC как радиусы окружности, углы ABO и ACO прямые по теореме об угле между радиусом и касательной, сторона AO общая. следовательно, прямоугольные треугольники равны по гипотенузе и катету, а значит, равны острые углы CAO и BAO. Следовательно, AO — биссектриса угла BAC, что и требовалось доказать.